在生产中，为了节约原材料，加工某些零件时常利用一些边角余料，如图，△ABC为锐角三角形废料．基中BC＝12cm，BC边上的高AD＝8cm，在△ABC上截取矩形PQMN，使QM与BC边重合，试说明P

Question

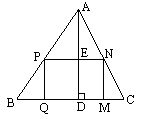
在生产中，为了节约原材料，加工某些零件时常利用一些边角余料，如图，△ABC为锐角三角形废料．基中BC＝12cm，BC边上的高AD＝8cm，在△ABC上截取矩形PQMN，使QM与BC边重合，试说明P，Q两点落在什么位置时，才可使它的面积S最大？最大值是多少？此时矩形的长和宽又各是多少？

Answer 1

答案：
解析：
　　[答案]如图，设PN交AD于E．PQ长为x(cm)，PN长为y cm．矩形的面积为S(cm2)．则AE＝(8－x)cm， 　　∵PN∥BC．∴∠APN＝∠ABC． 　　又∠PAN＝∠BAC，∴△APN∽△ABC．∴＝， 　　即＝．∴y＝(8－x)． 　　∴S＝PN·PQ＝xy＝(8－x)x＝－x2＋12x(0＜x＜8)． 　　即S＝－(x－4)2＋24． 　　∴当x＝4时，S有最大值24，此时y＝×(8－4)＝6cm． 　　此时＝＝＝＝，即P是AB的中点，Q是BD的中点． 　　故当P，Q分别为AB，BD的中点时，才可使矩形PQMN的面积最大，最大面积为24cm2，此时矩形的长为6cm，宽为4cm． 　　[剖析]先用字母x表示线段PQ的长，再运用相似三角形的性质，得到PN与x的函数关系式，从而用x的代数式表示PN的长，由此建立S与x之间的函数关系式，并用二次函数的相关知识解决问题，本题也可设AE长为x，同学们不妨试一试，并比较两种解决方式谁更优．
提示：
　　[方法提炼] 　　用x表示某一个量后，再运用相似形的性质或解直角三角形的知识或其他知识沟通其他量与x的关系，从而建立二次函数关系式表示实际问题，并运用二次函数的相关知识解决问题．