如图，二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3，1，则下列结论正确的个数有（）①ac>0；②2a-b=0；③4a-2b+c>0；④对于任意实数m均有am2+bm≥a-b．A.1B.2C.3D.4

Question

如图，二次函数y=ax²+bx+c的图象与x轴的交点的横坐标分别为-3，1，则下列结论正确的个数有（　　）
①ac>0；②2a-b=0；③4a-2b+c>0；④对于任意实数m均有am²+bm≥a-b．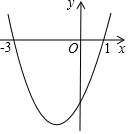

A. 1

B. 2

C. 3

D. 4

Answer 1

①∵抛物线开口向上且与y轴交于负半轴，即x=0时，y<0，
∴a>0、c<0，
∴ac<0，故此结论错误；

②∵抛物线与x轴交点的横坐标分别为-3、1，
∴x=-(b)/(2a)=(-3+1)/(2)，即2a+b=0，故此结论正确；

③由图象可知，当x=-2时，y<0，
∴4a-2b+c<0，故此结论错误；

④∵抛物线的对称轴为x=-1，且开口向上，
∴当x=-1时，二次函数取得最小值，
∴当x=m时，am²+bm+c≥a-b+c，即am²+bm≥a-b，故此结论正确；
故选：B．