如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的O与AD相切,点E为AD的中点,下列结论正确的个数是()(1)AB+CD=AD;(2)S△BCE=S△ABE+S△DCE;(3)AB•CD=14BC2;(4)∠ABE=∠DCE.A.
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的 O与AD相切,点E为AD的中点,下列结论正确的个数是( )
(1)AB+CD=AD;
(2)S△BCE=S△ABE+S△DCE;
(3)AB•CD=
BC2;1 4
(4)∠ABE=∠DCE.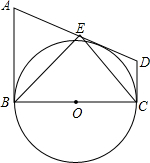
A. 1
B. 2
C. 3
D. 4
A、B、C、D、E都是短周期元素,原子半径D>C>A>E>B,其中A、B处在同一周期,A、C处在同 2020-04-08 …
高等代数题,我算得A+E必可逆,没有因果关系设矩阵A满足A^3=E,则有().A,若A-E可逆,则 2020-06-10 …
第一题令A={a,b,c,d,e},B={a,b,c,d,e,f,g,h}.求a)A∪Bb)A∩B 2020-06-17 …
A、B、C、D、E、F六个小朋友做游戏,每轮游戏都按照下面的箭头方向把原来手里的玩具传给另外一个小 2020-06-22 …
化学高手们帮帮我啊?超级急的啊!有A,B,C三种常见固体,投入水中分别产生D,E,F三种气体,他们 2020-06-23 …
设一数列a,b,c,d,e,f,通过栈结构不可能不可能排成的顺序数列为()A)c,b,e,f,d, 2020-06-28 …
A、B、C、D、E、F六个小朋友做游戏,每轮游戏都按照下面的箭头方向把原来手里的玩具传给另外一个小 2020-07-01 …
晶体管工作在放大区时的偏置状态为().A.b与e极,b与c极间均正向偏置B.b与e极,b与c极间均 2020-07-20 …
英语问题判断下列所给单词[]部分有几种读音1.A.dr[aw]B.[a]llC.fl[oor]D.b 2020-10-31 …
A是n阶方阵,且满足A^2=E,则下列结论正确的是()A:若A不等于E,则A+E不可逆B:若A不等于 2020-11-02 …