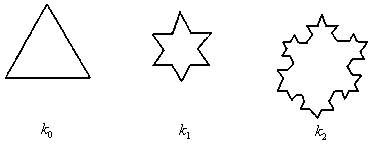
有一个雪花曲线序列，其产生的规则是：将正三角形k0的每一边三等分，而以其居中的那一线段为底边向外作等边三角形，再擦去中间的那条边，便得第一条雪花曲线k1

Question

有一个雪花曲线序列，其产生的规则是：将正三角形 k ₀ 的每一边三等分，而以其居中的那一线段为底边向外作等边三角形，再擦去中间的那条边，便得第一条雪花曲线 k ₁ ，再将 k ₁ 的每一边三等分，并重复上述作法，便得第二条雪花曲线 k ₂ …把 k _{n - 1} 的每一边三等分，并以中间那条线段向外作等边三角形， 再擦去中间的那条边， 便得第 n 条雪花曲线 k _n ( n = 2 ， 3 ， 4 ，… ) 。

（1） 　　   设 k ₀ 的周长为 L ₀ ，即正三角形的周长，求 k _n ，即第 n 条雪花曲线的周长 L _n ；

（2） 　　   设 k ₀ 的面积为 A ₀ ，即正三角形的面积，求 k _n 即第 n 条雪花曲线围成的面积 A _n ；

（ 3 ）随着 n 的增大， L _n 和 A _n 的极限是否存在？

 

 

Answer 1

答案：
解析：
（1）在雪花曲线序列中，将kn-1变为kn，后一曲线的同等是前一曲线同等的，∴ 的正三角形，k2比k1多出了3×4个面积为的正三角形，于是有 。 由 可得 (3)由。