早教吧作业答案频道 -->数学-->
如图①,在有公共顶点的△ABC和△ADE中,AB=AC,AD=AE,且∠CAB=∠EAD.(1)求证:CE=BD;(2)若将△ADE绕点A沿逆时针方向旋转使点C、E、D在同一条直线上时,如图②,(1)中的结论是否仍然
题目详情
如图①,在有公共顶点的△ABC和△ADE中,AB=AC,AD=AE,且∠CAB=∠EAD.
(1)求证:CE=BD;
(2)若将△ADE绕点A沿逆时针方向旋转使点C、E、D在同一条直线上时,如图②,(1)中的结论是否仍然成立?如果结论成立,请证明;如果结论不成立,请说明理由.
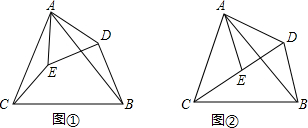
(1)求证:CE=BD;
(2)若将△ADE绕点A沿逆时针方向旋转使点C、E、D在同一条直线上时,如图②,(1)中的结论是否仍然成立?如果结论成立,请证明;如果结论不成立,请说明理由.

▼优质解答
答案和解析
(1)证明:∵∠CAB=∠EAD,
∴∠CAB-∠EAB=∠EAD-∠EAB,
∴∠CAE=∠BAD,
在△CAE和△BAD中
∴△CAE≌△BAD(SAS),
∴CE=BD;
(2)结论还成立,
证明:∵∠CAB=∠EAD,
∴∠CAB-∠EAB=∠EAD-∠EAB,
∴∠CAE=∠BAD,
在△CAE和△BAD中
∴△CAE≌△BAD(SAS),
∴CE=BD.
∴∠CAB-∠EAB=∠EAD-∠EAB,
∴∠CAE=∠BAD,
在△CAE和△BAD中
|
∴△CAE≌△BAD(SAS),
∴CE=BD;
(2)结论还成立,
证明:∵∠CAB=∠EAD,
∴∠CAB-∠EAB=∠EAD-∠EAB,
∴∠CAE=∠BAD,
在△CAE和△BAD中
|
∴△CAE≌△BAD(SAS),
∴CE=BD.
看了如图①,在有公共顶点的△ABC...的网友还看了以下:
已知等边△ABC,点D是直线BC上一点,以AD为边在AD的右侧作等边△ADE,连结CE.(1)如图 2020-05-13 …
探索新知如图1,点C将线段AB分成AC和BC两部分,若BC=πAC,则称点C是线段AB的圆周率点, 2020-06-14 …
如图,抛物线C1:y=ax2+bx-1与x轴交于两点A(-1,0),B(1,0),与y轴交于点C. 2020-06-14 …
已知抛物线y=4\3x²+bx+c经过A(3,0)、B(0,4)(1)求此抛物线的解析式;(2)若 2020-06-14 …
如图,点C是线段AB的中点.(1)若点D在线段CB上,且DB=3.5cm,AD=6.5cm,求线段 2020-06-15 …
在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.(1)如图1,若点 2020-06-23 …
新知理解如图①,点C在线段AB上,若BC=πAC,则称点C是线段AB的圆周率点,线段AC、BC称作 2020-07-03 …
CP是等边△ABC外角∠ACE平分线,点D在射线BC上,以D为顶点、DA为一边作角ADF=60°, 2020-07-17 …
点A,B,P在同一直线上,下列说法正确的是()A.若AB=2PA,则P是AB的中点B.若AB=PB 2020-07-18 …
已知,在三角形ABC中,D为直线AC上一点,角ABC=角ACB=x度,角ADF=角AFD=y度,直 2020-07-21 …