早教吧作业答案频道 -->数学-->
已知等边△ABC,点D是直线BC上一点,以AD为边在AD的右侧作等边△ADE,连结CE.(1)如图①,若点D在线段BC上,求证:CE+CD=AB;(2)如图②,若点D在BC延长线上,线段CD,CE和AB有怎样的数量关
题目详情
已知等边△ABC,点D是直线BC上一点,以AD为边在AD的右侧作等边△ADE,连结CE.
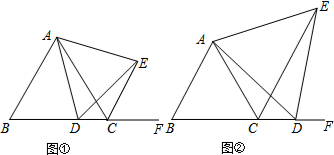
(1)如图①,若点D在线段BC上,求证:CE+CD=AB;
(2)如图②,若点D在BC延长线上,线段CD,CE和AB有怎样的数量关系?证明你的结论.
(1)如图①,若点D在线段BC上,求证:CE+CD=AB;
(2)如图②,若点D在BC延长线上,线段CD,CE和AB有怎样的数量关系?证明你的结论.

▼优质解答
答案和解析
证明:(1)如图①,∵△ADE与△ABC都是等边三角形,
∴AC=AB,AE=AD,∠DAE=∠BAC=60°.
∴∠DAE-∠CAD=∠BAC-∠CAD.
即∠CAE=∠BAD.
在△CAE和△BAD中,
,
∴△CAE≌△BAD(SAS).
∴EC=DB(全等三角形的对应边相等);
∴CE+CD=DB+CD=BC=AB,
即CE+CD=AB;
(2)CE-CD=AB;
理由如下:如图②,∵△ADE与△ABC都是等边三角形,
∴AC=AB,AE=AD,∠DAE=∠BAC=60°.
∴∠DAE+∠CAD=∠BAC+∠CAD.
即∠CAE=∠BAD.
在△CAE和△BAD中,
,
∴△CAE≌△BAD(SAS).
∴EC=DB(全等三角形的对应边相等);
∴CE-AB=DB-BC=CD,即CE-CD=AB.
∴AC=AB,AE=AD,∠DAE=∠BAC=60°.
∴∠DAE-∠CAD=∠BAC-∠CAD.

即∠CAE=∠BAD.
在△CAE和△BAD中,
|
∴△CAE≌△BAD(SAS).
∴EC=DB(全等三角形的对应边相等);
∴CE+CD=DB+CD=BC=AB,
即CE+CD=AB;
(2)CE-CD=AB;
理由如下:如图②,∵△ADE与△ABC都是等边三角形,
∴AC=AB,AE=AD,∠DAE=∠BAC=60°.
∴∠DAE+∠CAD=∠BAC+∠CAD.
即∠CAE=∠BAD.
在△CAE和△BAD中,
|
∴△CAE≌△BAD(SAS).
∴EC=DB(全等三角形的对应边相等);
∴CE-AB=DB-BC=CD,即CE-CD=AB.
看了 已知等边△ABC,点D是直线...的网友还看了以下:
(2010•金山区二模)如图,在Rt△ABC中,∠C=90°,AC=BC,D是AB边上一点,E是在 2020-06-08 …
如图,A,B,C,D,E五人围坐在圆桌旁,为A祝贺生日,小华问他们当时的座位.A说:“我在B的旁边 2020-06-12 …
已知D是等边△ABC边AB上的一点,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在A 2020-06-17 …
用两个一样的直角三角形和一个等腰直角三角形(腰等于前两个直角三角形的斜边)可以拼成一个直角梯形.如 2020-06-27 …
选出下列诗句中”野”的意思不一样的一句A.野无人舟自横B.山随平野尽,江入大荒流C.读出门前望野田 2020-06-28 …
(2006•南宁)如图是一个等边三角形木框,甲虫P在边框AC上爬行(A,C端点除外),设甲虫P到另 2020-07-12 …
如果凸n边形F(n≥4)的所有对角线都相等,那么A.F∈{四边形}B.F∈{五边形}C.F∈{四边 2020-07-25 …
如图.D为直线AB上一点,∠BOC=α.(1)如图①,若α=40°,OD平分∠AOC,∠DOE=9 2020-07-26 …
如图,已知△ABC的边BC长15厘米,高AH为10厘米,四边形DEFG内接于△ABC,点E、F在边 2020-07-26 …
如果要用下列边长相同的两种正多边形材料组合铺设地面,能平整镶嵌的组合方案是[]A.正四边形、正六边形 2020-11-02 …