早教吧作业答案频道 -->数学-->
抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线
题目详情
抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上.设抛物线y 2 =2px(p>0),弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为( )
A.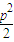
B.p 2
C.2p 2
D.4p 2
A.
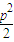
B.p 2
C.2p 2
D.4p 2
▼优质解答
答案和解析
分析:
法一:直接计算比较复杂,我们可以取几个特殊的位置,可得解.
法二:由于若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上,且△PAB为直角三角型,且角P为直角.又面积是直角边积的一半,斜边是两直角边的平方和,故可求.
法一:取倾斜角为:45 ,60 ,90 ,经计算可知,当倾斜角为90 时,△ABQ的面积的最小,此时AB=2p,又焦点到准线的距离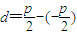 =p,此时三角形的面积最小为p 2 故选B.
=p,此时三角形的面积最小为p 2 故选B.
法二:由于若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上,且△PAB为直角三角型,且角P为直角.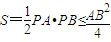 ,由于AB是通径时,AB最小,故选B.
,由于AB是通径时,AB最小,故选B.
点评:
本题作为选择题,采用特殊法,简单易行.由特殊求解一般性结论是解答选择题的一种很好的方法.△PAB称作阿基米德三角型.该三角形满足以下特性:1、P点必在抛物线的准线上;2、△PAB为直角三角型,且角P为直角;3、PF⊥AB(即符合射影定理)等.灵活利用性质是解题的关键.
分析:
法一:直接计算比较复杂,我们可以取几个特殊的位置,可得解.
法二:由于若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上,且△PAB为直角三角型,且角P为直角.又面积是直角边积的一半,斜边是两直角边的平方和,故可求.
法一:取倾斜角为:45 ,60 ,90 ,经计算可知,当倾斜角为90 时,△ABQ的面积的最小,此时AB=2p,又焦点到准线的距离
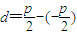 =p,此时三角形的面积最小为p 2 故选B.
=p,此时三角形的面积最小为p 2 故选B.法二:由于若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上,且△PAB为直角三角型,且角P为直角.
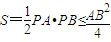 ,由于AB是通径时,AB最小,故选B.
,由于AB是通径时,AB最小,故选B.点评:
本题作为选择题,采用特殊法,简单易行.由特殊求解一般性结论是解答选择题的一种很好的方法.△PAB称作阿基米德三角型.该三角形满足以下特性:1、P点必在抛物线的准线上;2、△PAB为直角三角型,且角P为直角;3、PF⊥AB(即符合射影定理)等.灵活利用性质是解题的关键.
看了 抛物线的弦与过弦的端点的两条...的网友还看了以下:
在同一直线上的5个点可以确定的线段条数为(),可以确定的射线条数为(),可以确定的直线的条数为() 2020-05-14 …
2009绍兴数学中考16题李老师从油条的制作受到启发,设计了一个数学问题:如图,在数轴上截取从原点 2020-05-15 …
天花板比地板高2m的车厢里,悬挂着1m长的线,线端系者一个球,小车缓慢加速加速度为10m/s时细线 2020-05-17 …
一个长方形上画线,一条线最多能分2部分,两条线最多可以分4部分,3条线最多分4部分,那么N条线能分 2020-05-20 …
有九个银币,摆成三行三列,可以连出八条线,每条线上有三个银币.问:如何将这九个银币重新排列,使得可 2020-05-22 …
过一点的直线有()条,过两点的直线有()条.平面上三条直线两两香蕉,最多有()个交点,最少有()个 2020-05-23 …
过双曲线2x^2-y^2=16的右焦点作它的一条渐近线l1的垂线,过双曲线2x^2-y^2=16的 2020-06-04 …
在同一平面内,过一点可能有两条以上的直线与已知直线平行吗?任意画一条直线a,在直线外取点P,并过点 2020-06-06 …
3.(1)若一条直线上有两个点,则有线段条;若一条直线上有三个点,则有线段条;若一条直线上有四3. 2020-06-11 …
请问两条相交的直线最多有多少条对称轴老师说是4条,因为垂直时,一条直线是另一条直线的对称轴,但是老 2020-06-15 …