早教吧作业答案频道 -->数学-->
如图,在平行四边形ABCD中,AD=2CD,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论①∠DCF=∠ECF;②EF=CF;③∠DFE=3∠AEF;④S△BEC<2S△CEF.中一定成立的是.(请填序号
题目详情
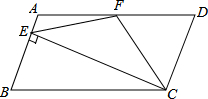
如图,在平行四边形ABCD中,AD=2CD,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论①∠DCF=∠ECF;②EF=CF;③∠DFE=3∠AEF;④S△BEC<2S△CEF.中一定成立的是___.(请填序号)

▼优质解答
答案和解析
如图延长EF交CD的延长线于H.作EN∥BC交CD于N,FK∥AB交BC于K.
∵四边形ABCD是平行四边形,
∴AB∥CH,
∴∠A=∠FDH,
在△AFE和△DFH中,
,
∴△AFE≌△DFH,
∴EF=FH,
∵CE⊥AB,AB∥CH,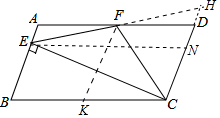
∴CE⊥CD,
∴∠ECH=90°,
∴CF=EF=FH,故②正确,
∵DF=CD=AF,
∴∠DFC=∠DCF=∠FCB,
∵∠FCB>∠ECF,
∴∠DCF>∠ECF,故①错误,
易证四边形DFKC是菱形,
∴∠DFC=∠KFC,
∵AE∥EK,
∴∠AEF=∠EFK,
∵FE=FC,FK⊥EC,
∴∠EFK=∠KFC,
∴∠DFE=3∠AEF,故③正确,
∵四边形EBCN是平行四边形,
∴S△BEC=S△ENC,
∵S△EHC=2S△EFC,S△EHC>S△ENC,
∴S△BEC<2S△CEF,故④正确,
故正确的有②③④.
故答案为②③④.
∵四边形ABCD是平行四边形,
∴AB∥CH,
∴∠A=∠FDH,
在△AFE和△DFH中,
|
∴△AFE≌△DFH,
∴EF=FH,
∵CE⊥AB,AB∥CH,

∴CE⊥CD,
∴∠ECH=90°,
∴CF=EF=FH,故②正确,
∵DF=CD=AF,
∴∠DFC=∠DCF=∠FCB,
∵∠FCB>∠ECF,
∴∠DCF>∠ECF,故①错误,
易证四边形DFKC是菱形,
∴∠DFC=∠KFC,
∵AE∥EK,
∴∠AEF=∠EFK,
∵FE=FC,FK⊥EC,
∴∠EFK=∠KFC,
∴∠DFE=3∠AEF,故③正确,
∵四边形EBCN是平行四边形,
∴S△BEC=S△ENC,
∵S△EHC=2S△EFC,S△EHC>S△ENC,
∴S△BEC<2S△CEF,故④正确,
故正确的有②③④.
故答案为②③④.
看了如图,在平行四边形ABCD中,...的网友还看了以下:
探究光的反射定律时,小强进行了如图的实验.(1)如图甲所示,当E、F在同一平面上时,让入射光线AO 2020-05-13 …
两个可导函数乘积是否可导?为什么?例题:f(x)在a,b上连续,在(a,b)内可导,且f(a)=0 2020-05-14 …
F浮=F下-F上;F下和F上分别是什么.请附F下的求值公式(请用文字表达) 2020-05-14 …
如果水中有石块,压强的计算公式一样吗?现在学习学到了浮力,但我蒙了.浮力是(F下-F上),但是F= 2020-05-16 …
物体在水中受力问题物体在水中会受到水各个方向的压强..F浮=F下-F上这个公式为什么没有考虑到物体 2020-05-16 …
运动员用双手握住竖直的竹竿匀速上攀和匀速下滑时,他所受的摩擦力分别为f上和f下,那么它们的关系是( 2020-07-04 …
如图1,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端 2020-07-25 …
f(x)是域F上的首一不可约多项式,域的特征CharF=0,设E是包含F的代数封闭域,由于f(x) 2020-07-27 …
设f(x),g(x)是数域F上的多项式,且a,b,c,d∈F,若ad-bc≠0,证明(af(x)设 2020-07-31 …
一切浸入液体中的物体,都受到液体的浮力作用.这句话不对吗?详解.网上说(浮力产生的原因是:浸在液体中 2020-11-03 …