早教吧作业答案频道 -->数学-->
如图,点E是正方形ABCD对角线AC上一点,EC=BC,过点E作FE⊥BE,交CD于点F(Ⅰ)∠BEC的度数等于.(Ⅱ)若正方形的边长为a,则CF的长等于.
题目详情
如图,点E是正方形ABCD对角线AC上一点,EC=BC,过点E作FE⊥BE,交CD于点F
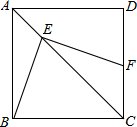
(Ⅰ)∠BEC的度数等于___.
(Ⅱ)若正方形的边长为a,则CF的长等于___.

(Ⅰ)∠BEC的度数等于___.
(Ⅱ)若正方形的边长为a,则CF的长等于___.
▼优质解答
答案和解析
(1)点E是正方形ABCD对角线AC上一点,
∴∠ACB=45°,
∵EC=BC,
∴∠BEC=∠EBC=
=67.5°
故答案为67.5°;
由(1)知,∠CBE=∠BEC=67.5°,
∴∠ABE=22.5°,
∵FE⊥BE,
∴∠BEF=90°,
∴∠CEF=22.5°,
∴∠ABE=∠CEF,
∵∠BAE=∠ECF,
∴△ABE和△CEF中
,
∴△ABE≌△CEF,
∴CF=AE,
∵正方形ABCD的边长为a,
∴AC=
a,
∵CE=AB=a,
∴CF=AE=AC-CE=
a-a=(
-1)a,
故答案为(
-1)a.
∴∠ACB=45°,
∵EC=BC,
∴∠BEC=∠EBC=
| 180°-∠ACB |
| 2 |
故答案为67.5°;
由(1)知,∠CBE=∠BEC=67.5°,
∴∠ABE=22.5°,
∵FE⊥BE,
∴∠BEF=90°,
∴∠CEF=22.5°,
∴∠ABE=∠CEF,
∵∠BAE=∠ECF,
∴△ABE和△CEF中
|
∴△ABE≌△CEF,
∴CF=AE,
∵正方形ABCD的边长为a,
∴AC=
| 2 |
∵CE=AB=a,
∴CF=AE=AC-CE=
| 2 |
| 2 |
故答案为(
| 2 |
看了如图,点E是正方形ABCD对角...的网友还看了以下:
对于正项数列{an},记Hn=/(a1+a2/2 +a3/3 +----+an/n ),若Hn=1 2020-05-16 …
判断下列指令语法书写是否正确,对于正确指令打√,并分别说明源操作数的寻址方式,对于错误指令打×,说 2020-05-16 …
现在,我国不少年轻人和孩子都喜欢过国外的“洋节”,对此,有人认为“对于外来节日和文化,我们不应盲目 2020-05-17 …
~~~~~~~~~~这个结论为什么不正确?~~~~~~~对于一元二次方程ax^2+bx+c=0(a 2020-05-23 …
为什么英语书上说”HELLO"是一句很不正式的用语?那怎样才算正式?对于非常熟悉的顾客,你可以用“ 2020-06-19 …
请教语文方面的问题“饺子对人充满诱惑”还是“人对饺子充满诱惑”,那种说法正确?有人说要把“对”改为 2020-06-19 …
对于任意实数X属于(1/8,1/7),代数式1-2X的绝对值+I1-3XI+I1-4XI+...+ 2020-07-10 …
|z1-z2|=根号(z1+z2)^2-4z1z2正确吗?看到网上的解答:本题的实质是|z|=√z 2020-08-02 …
真理一元论认为对于一个确定的对象是()A只能有一种认识B正确的认识只有一个C正确的认识能能一次D 2020-11-21 …
设凸透镜焦距为f,物距为u,像距为v,三者之间关系为,对于凸透镜,公式中的u和f为正值,实象v为正虚 2020-11-24 …