早教吧作业答案频道 -->物理-->
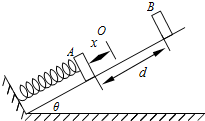
质量m=1.0kg的物块A(可视为质点)与轻弹簧的上端连接,弹簧下端固定在光滑斜面底端,斜面的倾斜角θ=30°.平衡时,弹簧的压缩量为x=0.20m,此时具有的弹性势能Ep=0.50J,物块A处在O时弹簧
题目详情
质量m=1.0kg的物块A(可视为质点)与轻弹簧的上端连接,弹簧下端固定在光滑斜面底端,斜面的倾斜角θ=30°.平衡时,弹簧的压缩量为x=0.20m,此时具有的弹性势能Ep=0.50J,物块A处在O时弹簧为原长,如图所示.一质量m=1.0kg物块B(可视为质点)从距离物块A为d=2.0m处从静止开始沿斜面下滑,与物体A发生碰撞后立刻一起向下运动,但不粘连,它们到达最低点后又向上运动.求物块B向上运动到达的最高点与O的距离s.g=10m/s2.

▼优质解答
答案和解析
B物体的加速度:a=
=gsinθ=5m/s2,
由匀变速直线运动的速度位移公式:v2=2ax可知,速度:v=
=2
m/s
AB碰撞过程系统动量守恒,以沿斜面向下为正方向,
根据动量守恒定律得:mv=2mv共,解得:v共=
m/s,
碰后AB和弹簧组成的系统,机械能守恒,并且AB在弹簧处分离,设AB分离瞬间速度为v′,
根据机械能守恒定律得:
2m
+EP=
2mv′2+2mgxsinθ,解得:v′=
m/s,
此后,B向上做匀减速运动,上升距离为:s=
=0.35m
即O与B运动的最高点之间的距离s为0.35米.
答:物块B向上运动到达的最高点与O的距离s为0.35m.
| mgsin30° |
| m |
由匀变速直线运动的速度位移公式:v2=2ax可知,速度:v=
| 2ad |
| 5 |
AB碰撞过程系统动量守恒,以沿斜面向下为正方向,
根据动量守恒定律得:mv=2mv共,解得:v共=
| 5 |
碰后AB和弹簧组成的系统,机械能守恒,并且AB在弹簧处分离,设AB分离瞬间速度为v′,
根据机械能守恒定律得:
| 1 |
| 2 |
| v | 2 共 |
| 1 |
| 2 |
| ||
| 2 |
此后,B向上做匀减速运动,上升距离为:s=
| v′2 |
| 2a |
即O与B运动的最高点之间的距离s为0.35米.
答:物块B向上运动到达的最高点与O的距离s为0.35m.
看了质量m=1.0kg的物块A(可...的网友还看了以下:
质量为m的木块,以一定的初速度v沿倾斜角为θ的斜面向上滑动,斜面静止不动,木块与质量为m的木块,以 2020-04-27 …
在m不能水平滑动与可以自由滑动两种情况下,m从顶端自由滑下,哪种情况先达底端M为一斜劈,顶端放一质 2020-05-13 …
高考物理如图所示,质量为M的楔形物块静止在水平地面,其斜面的倾角为θ.质量为m的小物块,如图所示, 2020-05-15 …
某物块以80J初动能从固定斜面底端上滑,以斜面底端为零势能参考平面,到达最高点时物块的重力势能为5 2020-06-12 …
m为何值时,经过俩点A(-m,6)B(1.3m)的直线的斜率是12 (2)m为何值时,经过俩点A( 2020-06-27 …
一个小物体m在沿斜面M向下的力F作用下沿斜面匀速下滑,斜劈受到地面的摩擦力为f与支持力为N则()A 2020-06-28 …
如图所示,质量为m=1kg的物块放在倾角为θ=37°的斜面体上,斜面质量为M=2kg,斜面与物块间 2020-07-17 …
已知M(2m+3,m),N(m-2,1).(1)当m为何值时,直线MN的倾斜角为锐角?(2)当m为 2020-07-30 …
(2013•湖北模拟)如图所示,质量为m的物体放在质量为M、倾角为θ的斜面体上,斜面体置于粗糙的水平 2020-11-05 …
如图所示,物体m在沿斜面向上的拉力F作用下沿斜面匀速下滑.此过程中斜面仍静止,斜面质量为M,则水平地 2020-12-15 …