早教吧作业答案频道 -->数学-->
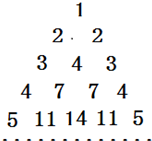
用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和,a(i+1)j=ai(j-1)+aij(i≥2,j≥2).设第n
题目详情
用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和,a(i+1)j=ai(j-1)+aij(i≥2,j≥2).设第n(n∈N+)行的第二个数为bn(n≥2).
(1)写出第7行的第三个数;
(2)写出bn+1与bn的关系并求bn(n≥2);
(3)设cn=2(bn-1)+n,证明:
+
+
+…+
<
.

(1)写出第7行的第三个数;
(2)写出bn+1与bn的关系并求bn(n≥2);
(3)设cn=2(bn-1)+n,证明:
| 1 |
| c2 |
| 1 |
| c4 |
| 1 |
| c6 |
| 1 |
| c2n |
| 1 |
| 2 |
▼优质解答
答案和解析
(1) 第7行的第三个数为41;
(2) 由已知得bn+1=bn+n,
∴当n≥2时,b3-b2=2,b4-b3=3,…,bn+1-bn=n,
累加,得:bn+1-b2=2+3+4+…+n,
∴bn+1=1+(1+2+3+4+…+n)=1+
,
∴bn=1+
(n≥2);
(3)证明:由(2)cn=2(bn-1)+n=n2,
∵
=
<
=
(
-
),
∴
+
+
+…+
<
(1-
)+
(
-
)+…
(
-
)=
(1-
)<
.
(2) 由已知得bn+1=bn+n,
∴当n≥2时,b3-b2=2,b4-b3=3,…,bn+1-bn=n,
累加,得:bn+1-b2=2+3+4+…+n,
∴bn+1=1+(1+2+3+4+…+n)=1+
| n(n+1) |
| 2 |
∴bn=1+
| n(n-1) |
| 2 |
(3)证明:由(2)cn=2(bn-1)+n=n2,
∵
| 1 |
| c2k |
| 1 |
| 4k2 |
| 1 |
| 4k2-1 |
| 1 |
| 2 |
| 1 |
| 2k-1 |
| 1 |
| 2k+1 |
∴
| 1 |
| c2 |
| 1 |
| c4 |
| 1 |
| c6 |
| 1 |
| c2n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
看了用部分自然数构造如图的数表:用...的网友还看了以下:
(2012•长宁区二模)做圆周运动的两个物体M和N,它们所受的向心力F与轨道半径R之间的关系如图所 2020-06-16 …
如图所示,有两个小球M和N,密度分别为ρM和ρN.图甲中,细线的一端固定在杯底,另一端拴住小球M使 2020-06-29 …
指南针是我国古代的四大发明之一.当指南针静止时,其N极指向如图虚线(南北向)所示,若某一条件下该指 2020-07-08 …
如图所示,有两个小球M和N,密度分别为ρM和ρN.图甲中,细线的一端固定在杯底,另一端拴住小球M使 2020-07-11 …
设A是三阶非零实矩阵,其元素aij与A的代数余子式Aij相等,求|A| 2020-07-16 …
指南针是我国古代的四大发明之一,当指南针静止时,由于地磁场使其N极指向如图中虚线(南北向),当在指 2020-07-22 …
观察如图的图形,找规律,填表答题.小梯形个数n1234…n图形的边数a47…(1)把表补充完整,并 2020-08-01 …
设A为n阶实对称矩阵,秩(A)=n,Aij是A=(aij)n×ij中元素aij的代数余子式(i,j 2020-08-03 …
设n阶行列式D=|aij|n,Aij是D中元素aij的代数余子式,则下列各式中正确的是()A.ni 2020-08-03 …
(满分12分)某专卖店销售一新款服装,日销售量(单位为件)f(n)与时间n(1≤n≤30、nÎN*) 2020-11-14 …