早教吧作业答案频道 -->数学-->
已知:△ABC是等边三角形.(1)如图1,点D在AB边上,点E在AC边上,BD=CE,BE与CD交于点F.试判断BF与CF的数量关系,并加以证明;(2)点D是AB边上的一个动点,点E是AC边上的一个动点,且BD=
题目详情
已知:△ABC是等边三角形.
(1)如图1,点D在AB边上,点E在AC边上,BD=CE,BE与CD交于点F. 试判断BF与CF的数量关系,并加以证明;
(2)点D是AB边上的一个动点,点E是AC边上的一个动点,且BD=CE,BE与CD交于点F.若△BFD是等腰三角形,求∠FBD的度数.
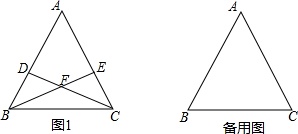
(1)如图1,点D在AB边上,点E在AC边上,BD=CE,BE与CD交于点F. 试判断BF与CF的数量关系,并加以证明;
(2)点D是AB边上的一个动点,点E是AC边上的一个动点,且BD=CE,BE与CD交于点F.若△BFD是等腰三角形,求∠FBD的度数.

▼优质解答
答案和解析
(1)BF=CF;理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
在△BCD和△CBE中,
,
∴△BCD≌△CBE(SAS),
∴∠BCD=∠CBE,
∴BF=CF.
(2)由(1)得:∠BCD=∠CBE,∠ACB=60°,
设∠BCD=∠CBE=x,
∴∠DBF=60°-x,
若△BFD是等腰三角形,分三种情况:
①若FD=FB,则∠FBD=∠FDB>∠A,
∴∠FBD=∠FDB>60°,
但∠FBDxy∠ABC,
∴∠FBD<60°,
∴FD=FB的情况不存在;
 ②若DB=DF,则∠FBD=∠BFD=2x,
②若DB=DF,则∠FBD=∠BFD=2x,
∴60°-x=2x,
解得:x=20°,
∴∠FBD=40°;
③若BD=BF,如图所示:
则∠BDF=∠BFD=2x,
在△BDF中,∠DBF+∠BDF+∠BFD=180°,
∴60°-x+2x+2x=180°,
解得:x=40°,
∴∠FBD=20°;
综上所述:∠FBD的度数是40°或20°.
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
在△BCD和△CBE中,
|
∴△BCD≌△CBE(SAS),
∴∠BCD=∠CBE,
∴BF=CF.
(2)由(1)得:∠BCD=∠CBE,∠ACB=60°,
设∠BCD=∠CBE=x,
∴∠DBF=60°-x,
若△BFD是等腰三角形,分三种情况:
①若FD=FB,则∠FBD=∠FDB>∠A,
∴∠FBD=∠FDB>60°,
但∠FBDxy∠ABC,
∴∠FBD<60°,
∴FD=FB的情况不存在;
 ②若DB=DF,则∠FBD=∠BFD=2x,
②若DB=DF,则∠FBD=∠BFD=2x,∴60°-x=2x,
解得:x=20°,
∴∠FBD=40°;
③若BD=BF,如图所示:
则∠BDF=∠BFD=2x,
在△BDF中,∠DBF+∠BDF+∠BFD=180°,
∴60°-x+2x+2x=180°,
解得:x=40°,
∴∠FBD=20°;
综上所述:∠FBD的度数是40°或20°.
看了 已知:△ABC是等边三角形....的网友还看了以下:
关于平均数1.什么叫算术平均数?什么叫几何平均数?2.利用它们的性质解题:(1)一个矩形的四边AB 2020-04-09 …
数学的问题已知△ABC中,BC=a,BC边上的高AH=h;矩形DEFG的定点D,E在边BC上,定点 2020-05-14 …
求三角形的度数,A边长100,B长100,c长19,求AB夹角是多少度?公式? 2020-06-03 …
李伟家客厅长6米,宽4.8米,计划在地面上铺方砖,选择一种方砖,使地面都是整块数A.边长50厘米B 2020-06-26 …
如图,点D为△ABC边AB的中点,将△ABC沿经过点D的直线折叠,使点A刚好落在BC边上的点F处, 2020-07-16 …
三角形选择题1.下列各角度数不能作为正多边形的内角度数的是()A.136B.144C.(128又4 2020-07-17 …
1.下列多边形材料中,不能单独用来铺满地面的是a,正三角形b.正4边形c.正5边形.d.正6边形. 2020-07-30 …
1.用两种正多边形铺地,不能匹配的三角形是?(说明原因)A.正方形B.正六边形C.正十二边形D.正 2020-08-02 …
下列说法正确的是()A.一个多边形外角的个数与边数相同B.一个多边形外角的个数是边数的2倍C.每个 2020-08-02 …
如图,在三角形ABC中,AB=AC=5,BC=6点D为AB边上的一动点(D不与A、B重合),过D作D 2021-01-11 …