（2012年5月南京、盐城三模）如图所示，有一个可视为质点的质量为m=1kg的小物块，从光滑平台上的A点以v0=3m/s的初速度水平抛出，到达C点时，恰

Question

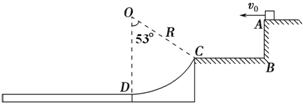
（ 2012 年 5 月南京、盐城三模）如图所示，有一个可视为质点的质量为 m = 1 kg 的小物块，从光滑平台上的 A 点以 v ₀ = 3 m/s 的初速度水平抛出，到达 C 点时，恰好沿 C 点的切线方向进入固定在水平地面上的光滑圆弧轨道，最后小物块滑上紧靠轨道末端 D 点的质量为 M = 3 kg 的长木板．已知木板上表面与圆弧轨道末端切线相平，木板下表面与水平地面之间光滑，小物块与长木板间的动摩擦因数 μ = 0.3 ，圆弧轨道的半径为 R = 0.5m ， C 点和圆弧的圆心连线与竖直方向的夹角 θ = 53° ，不计空气阻力，取重力加速度为 g = 10 m /s ² . 求：

⑴ AC 两点的高度差；

⑵ 小物块刚要到达圆弧轨道末端 D 点时对轨道的压力；

⑶ 要使小物块不滑出长木板，木板的最小长度 ．

（ sin53 ° =0.8 ， cos53 ° =0.6 ）

Answer 1

解析：⑴ 小物块在 C 点时的速度大小为 v _C = = 5 m /s ，竖直分量为 v _Cy = 4 m/s （ 2 分）     下落高度 h = v _Cy ² /2 g = 0.8m   （ 2 分）

⑶ 设小物块刚滑到木板左端达到共同速度，大小为 v ，小物块在木板上滑行的过程中，小物块与长木板的加速度大小分别为

a ₁ = μg = 3 m /s ² ， a ₂ =  = 1 m /s ² （ 1 分）

速度分别为 v = v _D – a ₁ t ， v = a ₂ t   （ 1 分）

对物块和木板系统，由能量守恒定律得：

μmgL = m v – ( m ＋ M ) v ²   （ 2 分）

解得 L = 3.625 m ，即木板的长度至少是 3.625 m （ 1 分）