某养殖场原有一块直角梯形的水域ABCD，其中BC，AD与边AB垂直，AD=800m，AB=2BC=600m．为满足钓鱼爱好者需要，计划修建两道互相垂直的水上栈道MF与ME，点M，E，F都在岸边上，其中M为AB的中点，

Question

某养殖场原有一块直角梯形的水域ABCD，其中BC，AD与边AB垂直，AD=800m，AB=2BC=600m．为满足钓鱼爱好者需要，计划修建两道互相垂直的水上栈道MF与ME，点M，E，F都在岸边上，其中M为AB的中点，点E在岸边BC上，设∠EMB=θrad，水上栈道MF与ME的长度和记为f（θ）（单位：m）．

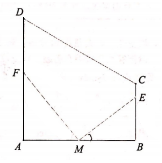
（1）写出f（θ）关于θ的函数关系式，并指出tanθ的范围；
（2）求f（θ）的最小值，并求出此时θ的值．

Answer 1

（1）梯形ABCD中，BC⊥AB，AD∥BC，AD=800m，AB=2BC=600m；
MF⊥ME，且M为AB的中点，点E在BC上，设∠EMB=θ，则0<θ≤45°；
∴ME=(MB)/(cosθ)=(300)/(cosθ)，
MF=(MA)/(cos(90°-θ))=(300)/(sinθ)，
∴f（θ）=(300)/(cosθ)+(300)/(sinθ)，其中0°<θ≤45°，
∴0<tanθ≤1；
（2）由f（θ）=(300)/(cosθ)+(300)/(sinθ)，
得f′（θ）=300（(sinθ)/(cos2θ)-(cosθ)/(sin2θ)）=300•(sin3θ-cos3θ)/(sin2θcos2θ)，
令f′（θ）=0，解得sinθ=cosθ，
∴θ=45°，且0°<θ<45°时，f′（θ）<0，f（θ）单调递减；
∴θ=45°时，f（θ）=(300)/((√(2))/(2))+(300)/((√(2))/(2))=600√(2)，为最小值．