早教吧作业答案频道 -->数学-->
已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.(1)如图1,求证:△AFB≌△ADC;(2)请判断图1
题目详情
已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
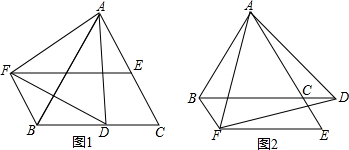
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.

▼优质解答
答案和解析
证明:(1)∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD-∠BAD,∠DAC=∠BAC-∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
,
∴△AFB≌△ADC(SAS);
(2)由①得△AFB≌△ADC,
∴∠ABF=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABF=∠BAC,
∴FB∥AC,
又∵BC∥EF,
∴四边形BCEF是平行四边形;
(3)成立,理由如下:
∵△ABC和△ADE都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD-∠BAD,∠DAC=∠BAC-∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
,
∴△AFB≌△ADC(SAS);
∴∠AFB=∠ADC.
又∵∠ADC+∠DAC=60°,∠EAF+∠DAC=60°,
∴∠ADC=∠EAF,
∴∠AFB=∠EAF,
∴BF∥AE,
又∵BC∥EF,
∴四边形BCEF是平行四边形.
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD-∠BAD,∠DAC=∠BAC-∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
|
∴△AFB≌△ADC(SAS);
(2)由①得△AFB≌△ADC,
∴∠ABF=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABF=∠BAC,
∴FB∥AC,
又∵BC∥EF,
∴四边形BCEF是平行四边形;
(3)成立,理由如下:
∵△ABC和△ADE都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD-∠BAD,∠DAC=∠BAC-∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
|
∴△AFB≌△ADC(SAS);
∴∠AFB=∠ADC.
又∵∠ADC+∠DAC=60°,∠EAF+∠DAC=60°,
∴∠ADC=∠EAF,
∴∠AFB=∠EAF,
∴BF∥AE,
又∵BC∥EF,
∴四边形BCEF是平行四边形.
看了已知△ABC是等边三角形,D是...的网友还看了以下:
初中一年级的直角三角形试题计算请高手在三角形中角等于90度,AC等于6,BC等于8,AB等于10点 2020-04-26 …
三角形ABC是等边三角形,AM⊥BC于M,PD⊥AD于D,PE⊥AC于E,PD=h1,PE=h2, 2020-06-04 …
已知:在三角形ABC中,角C=90度,CM垂直AB于M,AT平分角BAC交CM于D,交BC于T,过 2020-07-17 …
E为三角形ABC中AB边的中点,D为三角形ABC外一点,E为三角形ABC中AB边的重点,D为三角形 2020-07-22 …
设d是三角形ABC的边AB上一点作DE平行BC交AC于E作DF平行ACBCFADEDBFmnDEC 2020-07-22 …
一个三角形ABC,角A为60度,角B角C的角平分线分别交AB于D交AC于E两线交于点F连接D,E有 2020-07-30 …
请在这里概述您的问题三角形ABC的角平分线AD,BE分别交BC,CA于点D,E,DE平分∠ADC, 2020-08-02 …
下面说法错误的是()A.三角形的三条角平分线交于一点B.三角形的三条中线交于一点C.三角形的三条高 2020-08-02 …
如图,在三棱柱...接上,三棱柱ABC-A'B'C'中,D为BC上一点,且A'B平行于平面AC'D. 2020-11-03 …
等边三角形内置三角尺旋转等边三角形ABC边长为3CM,(BC水平位置.A在上方)点D在三角形的外部( 2021-01-04 …