早教吧作业答案频道 -->数学-->
已知如图,在四边形ABCD中,AD=CD,M、N分别是BC、AB上的点.(1)如图①,若∠A=∠C=90°,∠B=∠MDN=60°.某同学在探究线段AN、MN、CM之间的数量关系时是这样的思路:延长BA到P,使AP=CM,
题目详情
已知如图,在四边形ABCD中,AD=CD,M、N分别是BC、AB上的点.
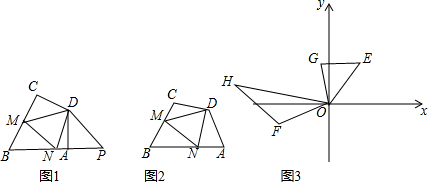
(1)如图①,若∠A=∠C=90°,∠B=∠MDN=60°.某同学在探究线段AN、MN、CM之间的数量关系时是这样的思路:延长BA到P,使AP=CM,连接PD(图1中虚线),通过研究图中有关三角形全等,再利用全等三角形的性质结合题中条件进行转化,从而得到结论.
这位同学在这个研究过程中:证明两对三角形分别全等的依据是___,得出线段AN、MN、CM之间的数量关系的结论是___.
(2)如图②,若∠A+∠C=180°,其他条件不变,当AN、MN、CM之间满足(1)中的数量关系时,设∠B=α°,请求出∠MDN的度数(用α含的代数式表示);
(3)如图③,我区某学校在庆祝“六一”儿童节的定向越野活动中,大本营指挥部设在点O处,甲同学在指挥部东北方向的E处,乙同学在指挥部南偏西75°的F处,且两位同学到指挥部的距离相等.接到行动指令后,甲同学以100米/分钟的速度向正西方向前进,乙同学以120米/分钟的速度向北偏西60°方向前进.10分钟后,指挥部监测到甲、乙两同学分别到达G、H处,且么∠GOH=75°,求此时甲、乙两同学之间的距离.
(1)如图①,若∠A=∠C=90°,∠B=∠MDN=60°.某同学在探究线段AN、MN、CM之间的数量关系时是这样的思路:延长BA到P,使AP=CM,连接PD(图1中虚线),通过研究图中有关三角形全等,再利用全等三角形的性质结合题中条件进行转化,从而得到结论.
这位同学在这个研究过程中:证明两对三角形分别全等的依据是___,得出线段AN、MN、CM之间的数量关系的结论是___.
(2)如图②,若∠A+∠C=180°,其他条件不变,当AN、MN、CM之间满足(1)中的数量关系时,设∠B=α°,请求出∠MDN的度数(用α含的代数式表示);
(3)如图③,我区某学校在庆祝“六一”儿童节的定向越野活动中,大本营指挥部设在点O处,甲同学在指挥部东北方向的E处,乙同学在指挥部南偏西75°的F处,且两位同学到指挥部的距离相等.接到行动指令后,甲同学以100米/分钟的速度向正西方向前进,乙同学以120米/分钟的速度向北偏西60°方向前进.10分钟后,指挥部监测到甲、乙两同学分别到达G、H处,且么∠GOH=75°,求此时甲、乙两同学之间的距离.

▼优质解答
答案和解析
(1)如图1,
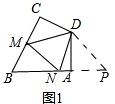
延长BA到P,使AP=CM,连接PD,
∵∠BAD=∠C=90°,
∴∠DAP=90°,
在△CDM和△ADP中
,
∴△CDM≌△ADP(SAS),
∴DM=DP,∠CDM=∠ADP,
在四边形ABCD中,∠C=∠BAD=90°,∠B=60°,
∴根据四边形的内角和得,∠ADC=120°,
∵∠MDN=60°,
∴∠CDM+∠ADN=60°,
∵∠CDM=∠ADP,
∴∠MDN=∠PDN,
在△DMN和△DPN中,
,
∴△DMN≌△DPN(SAS),
∴MN=PN=AN+AP=AN+CM;
故答案为:SAS,SAS,MN=AN+CM
(2)如图2,
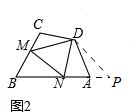
延长BA到P,使AP=CM,连接PD,
∵∠BAD+∠C=180°,∠BAD+∠DAP=180°,
∴∠C=∠DAP,
在△CDM和△ADP中
,
∴△CDM≌△ADP(SAS),
∴DM=DP,∠CDM=∠ADP,
∵CM=AP,
∴MN=AN+CM=AN+AP=PN,
在△DMN和△DPN中,
∴△DMN≌△DPN(SSS),
∴∠MDN=∠PDN=∠ADP+∠ADN,
∵∠CDM=∠ADP,
∴∠MDN=∠CDM+∠ADN=
∠ADC,
在四边形ABCD中,∠BAD+∠C=180°,
∴根据四边形的内角和得,∠B+∠ADC=180°,
∴∠B+2∠MDN=180°,
∵∠B=α,
∴∠MDN=
=90°-
α.
(3)如图3,
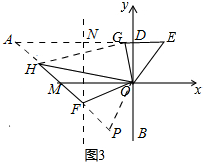
延长EG,FH相较于点A,过点F作FN⊥AE,
∴乙同学以120米/分钟的速度向北偏西60°方向前进,
∴∠NFA=60°,
∴∠A=30°,
∵甲同学在指挥部东北方向的E处,乙同学在指挥部南偏西75°的F处,
∴∠DOE=45°,∠BOF=75°,
∴∠MOF=90°-75°=15°,
∴∠EOF=∠DOE+∠DOM+MOF=150°,
∴∠A+∠EOF=180°,
延长AF至点P,使FP=GE,
满足(1)的条件,则有HG=HP=HF+FP,
∵甲同学以100米/分钟的速度向正西方向前进,乙同学以120米/分钟的速度向北偏西60°方向前进.10分钟后,指挥部监测到甲、乙两同学分别到达G、H处,
∴GE=100×10=1000米,HF=120×10=1200米,
∴HG=HF+FP=1200+1000=2200米,
即:甲、乙两同学之间的�

延长BA到P,使AP=CM,连接PD,
∵∠BAD=∠C=90°,
∴∠DAP=90°,
在△CDM和△ADP中
|
∴△CDM≌△ADP(SAS),
∴DM=DP,∠CDM=∠ADP,
在四边形ABCD中,∠C=∠BAD=90°,∠B=60°,
∴根据四边形的内角和得,∠ADC=120°,
∵∠MDN=60°,
∴∠CDM+∠ADN=60°,
∵∠CDM=∠ADP,
∴∠MDN=∠PDN,
在△DMN和△DPN中,
|
∴△DMN≌△DPN(SAS),
∴MN=PN=AN+AP=AN+CM;
故答案为:SAS,SAS,MN=AN+CM
(2)如图2,

延长BA到P,使AP=CM,连接PD,
∵∠BAD+∠C=180°,∠BAD+∠DAP=180°,
∴∠C=∠DAP,
在△CDM和△ADP中
|
∴△CDM≌△ADP(SAS),
∴DM=DP,∠CDM=∠ADP,
∵CM=AP,
∴MN=AN+CM=AN+AP=PN,
在△DMN和△DPN中,
|
∴△DMN≌△DPN(SSS),
∴∠MDN=∠PDN=∠ADP+∠ADN,
∵∠CDM=∠ADP,
∴∠MDN=∠CDM+∠ADN=
| 1 |
| 2 |
在四边形ABCD中,∠BAD+∠C=180°,
∴根据四边形的内角和得,∠B+∠ADC=180°,
∴∠B+2∠MDN=180°,
∵∠B=α,
∴∠MDN=
| 180°-α |
| 2 |
| 1 |
| 2 |
(3)如图3,

延长EG,FH相较于点A,过点F作FN⊥AE,
∴乙同学以120米/分钟的速度向北偏西60°方向前进,
∴∠NFA=60°,
∴∠A=30°,
∵甲同学在指挥部东北方向的E处,乙同学在指挥部南偏西75°的F处,
∴∠DOE=45°,∠BOF=75°,
∴∠MOF=90°-75°=15°,
∴∠EOF=∠DOE+∠DOM+MOF=150°,
∴∠A+∠EOF=180°,
延长AF至点P,使FP=GE,
满足(1)的条件,则有HG=HP=HF+FP,
∵甲同学以100米/分钟的速度向正西方向前进,乙同学以120米/分钟的速度向北偏西60°方向前进.10分钟后,指挥部监测到甲、乙两同学分别到达G、H处,
∴GE=100×10=1000米,HF=120×10=1200米,
∴HG=HF+FP=1200+1000=2200米,
即:甲、乙两同学之间的�
看了已知如图,在四边形ABCD中,...的网友还看了以下:
读“某日某时地球可见光云图”(白色为云层),完成1~2题。1.此时为A.冬至日前后B.夏至日前后C 2020-05-04 …
高一集合题中有个B=φ是什么意思/已知集合A={x|x2-1=0},B={x|ax+2=0}时,并 2020-05-13 …
图为北极地区俯视图,阴影部分表示黑夜。依图判断1~2题。1.此时北京时间可能是①6月22日12时② 2020-06-10 …
从下列句子中各找出一对反义词,并写下来。1.有时候我很温和,有时候我很暴躁。()——()2.从下列 2020-07-04 …
读“世界某区域轮廓图”,图中虚线MN为晨昏线,此时乙岛东北部降水量大于西南部。完成1-3题。1.此 2020-07-05 …
1,2,3,三人同时从a地向b地跑,当1到B时,2离B地还有20米,3离还有B地40米,当2到B时 2020-07-12 …
如图所示,一质点在x轴上以O为平衡位置做简谐运动,其振幅为8cm,周期为4s.t=0时物体在x=4 2020-07-13 …
读下图,M、N是晨昏线与某纬线的交点,MN垂直于OE,P为MN的中点。回答1~3题。1.此时世界时 2020-07-15 …
两辆汽车均在水平公路上匀速行驶,在相等的时间内通过的距离之比为2:1.若两车的发动机的输出功率相等 2020-07-20 …
已知函数f(x)=ln(x+1)+ax2-x,a∈R.(Ⅰ)当a=14时,求函数y=f(x)的极值 2020-07-27 …