早教吧作业答案频道 -->数学-->
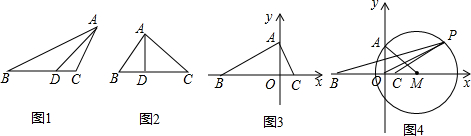
如图1,对△ABC,D是BC边上一点,连结AD,当AB2AC2=BDCD时,称AD为BC边上的“平方比线”.同理AB和AC边上也存在类似的“平方比线”.(1)如图2,△ABC中,∠BAC=RT∠,AD⊥BC于D.证明:AD为BC边
题目详情
如图1,对△ABC,D是BC边上一点,连结AD,当
=
时,称AD为BC边上的“平方比线”.同理AB和AC边上也存在类似的“平方比线”.
(1)如图2,△ABC中,∠BAC=RT∠,AD⊥BC于D.
证明:AD为BC边上的“平方比线”;
(2)如图3,在平面直角坐标系中,B(-4,0),C(1,0),在y轴的正半轴上找一点A,使OA是△ABC中BC边上的“平方比线”.
①求出点A的坐标;
②如图4,以M(
,0)为圆心,MA为半径作圆,在 M上任取一点P(与x轴交点除外)吗,连结PB,PC,PO.求证:PO始终是△PBC中BC边上的“平方比线”.
| AB2 |
| AC2 |
| BD |
| CD |
(1)如图2,△ABC中,∠BAC=RT∠,AD⊥BC于D.
证明:AD为BC边上的“平方比线”;
(2)如图3,在平面直角坐标系中,B(-4,0),C(1,0),在y轴的正半轴上找一点A,使OA是△ABC中BC边上的“平方比线”.
①求出点A的坐标;
②如图4,以M(
| 8 |
| 3 |

▼优质解答
答案和解析
(1)∵∠BAC=RT∠,
∴∠B+∠C=90°,
∵AD⊥BC,
∴∠B+∠BAD=90°,
∴∠BAD=∠C,
∵∠BDA=∠BAC=90°,
∴△BAD∽△BCA,
∴
=
,
∴AB2=BD×BC,
同理可得;AC2=CD×BC,
∴
=
,
∴AD为BC边上的“平方比线”.
(2)①设A(0,m)(m>0),
则OA=m,而OB=4,OC=1,
所以AB2=m2+16,AC2=m2+1,
∵OA为BC边上的“平方比线”,
∴
=
,
∴
=4,
解得:m=2
∴A(0,2).
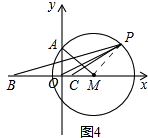
②证明:连结PM,如图4,
则PM=AM=
=
,
∵MC×MB=
×
=
=PM2,
∴
=
,
∵∠PMC=∠PMB,
∴△MPC∽△MBP,
∴
=
=
∴
=
=
∴PO始终是BC边上的“平方比线”.
∴∠B+∠C=90°,
∵AD⊥BC,
∴∠B+∠BAD=90°,
∴∠BAD=∠C,
∵∠BDA=∠BAC=90°,
∴△BAD∽△BCA,
∴
| AB |
| BC |
| BD |
| AB |
∴AB2=BD×BC,
同理可得;AC2=CD×BC,
∴
| AB2 |
| AC2 |
| BD |
| CD |
∴AD为BC边上的“平方比线”.
(2)①设A(0,m)(m>0),
则OA=m,而OB=4,OC=1,
所以AB2=m2+16,AC2=m2+1,
∵OA为BC边上的“平方比线”,
∴
| AB2 |
| AC2 |
| BO |
| CO |
∴
| m2+16 |
| m2+1 |
解得:m=2
∴A(0,2).
②证明:连结PM,如图4,

则PM=AM=
(
|
| 10 |
| 3 |
∵MC×MB=
| 5 |
| 3 |
| 20 |
| 3 |
| 100 |
| 9 |
∴
| PM |
| MC |
| MB |
| PM |
∵∠PMC=∠PMB,
∴△MPC∽△MBP,
∴
| PC |
| BP |
| MC |
| PM |
| 1 |
| 2 |
∴
| PC2 |
| BP2 |
| 1 |
| 4 |
| OC |
| OB |
∴PO始终是BC边上的“平方比线”.
看了如图1,对△ABC,D是BC边...的网友还看了以下:
已知(如图所示)A(3,2),B(3,4),C(-4,-2),D(2,-2),(1)A与B是对称点 2020-05-02 …
定义:如果一元二次方程 ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“凤 2020-05-15 …
在社交场合,称谓对方为“校长先生”,这属于( )。A.职务称 B.一般称 C.职业称 D.代词称 2020-05-19 …
在社交场合,称谓对方为“校长先生”,这属于( )。 A.职务称B.一般称C.职业称D.代词称 2020-05-20 …
在社交场合,称呼对方为“校长先生”,这属于( )。 A.职务称 B.一般称 C.职业称 D.代词称 2020-05-20 …
在社交场合,称谓对方为“校长先生”,这属于( )。A.职务称B.一般称C.职业称D.代词称 2020-05-20 …
如图,正方形ABCD的边长为2cm,在对称中心O处有一钉子.动点P,Q同时从点A出发,点P沿A⇒B 2020-05-22 …
设A是n阶方阵(不一定是对称阵),二次型f(x)=xTAx相对应的对称阵是()注:T代表转置(A) 2020-06-18 …
在农业生产上,需用15%的氯化钠溶液1000g来选种,下述方法中正确的是()A.称取15g氯化钠, 2020-07-09 …
方程x*2-3xy-y*2=4的曲线A关于x轴对称B关于y轴对称C关于原点对称D无对称轴或对称中心 2020-07-20 …