如图，甲、乙两人想在正五边形ABCDE内部找一点P，使得四边形ABPE为平行四边形，其作法如下：（甲）连接BD、CE，两线段相交于P点，则P即为所求（乙）先取CD的中点M，再以A为圆心，AB长

Question

如图，甲、乙两人想在正五边形ABCDE内部找一点P，使得四边形ABPE为平行四边形，其作法如下：
（甲） 连接BD、CE，两线段相交于P点，则P即为所求
（乙） 先取CD的中点M，再以A为圆心，AB长为半径画弧，交AM于P点，则P即为所求．
对于甲、乙两人的作法，下列判断何者正确？（　　）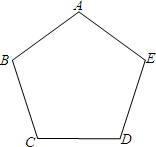

A. 两人皆正确

B. 两人皆错误

C. 甲正确，乙错误

D. 甲错误，乙正确

Answer 1

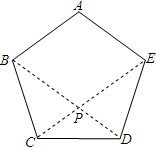
甲正确，乙错误，
理由是：如图，∵正五边形的每个内角的度数是((5-2)×180°)/(5)=108°，AB=BC=CD=DE=AE，
∴∠DEC=∠DCE=(1)/(2)×（180°-108°）=36°，
同理∠CBD=∠CDB=36°，
∴∠ABP=∠AEP=108°-36°=72°，
∴∠BPE=360°-108°-72°-72°=108°=∠A，
∴四边形ABPE是平行四边形，即甲正确；

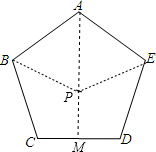
∵∠BAE=108°，
∴∠BAM=∠EAM=54°，
∵AB=AE=AP，
∴∠ABP=∠APB=(1)/(2)×（180°-54°）=63°，∠AEP=∠APE=63°，
∴∠BPE=360°-108°-63°-63°≠108°，
即∠ABP=∠AEP，∠BAE≠∠BPE，
∴四边形ABPE不是平行四边形，即乙错误；
故选C．