如图，已知平行六面体ABCD-的底面ABCD是菱形，且=。（I）证明：⊥BD；（II）当的值为多少时，能使平面？

Question

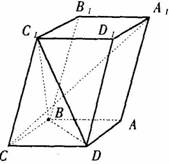如图，已知平行六面体 ABCD- 的底面 ABCD 是菱形，且 = 。

（ I ）证明： ⊥ BD ；

    （ II ）当 的值为多少时，能使 平面 ？请给出证明。

Answer 1

本小题主要考查直线与直线、直线与平面的关系，逻辑推理能力 .

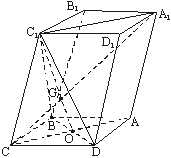
  （ Ⅰ ）证明：连结 A ₁ C ₁ 、 AC ， AC 和 BD 交于 O ，连结 C ₁ O .

∵ 四边形 ABCD 是菱形， ∴ AC ⊥ BD ， BC ＝ CD .

又 ∵∠ BCC ₁ ＝ ∠ DCC ₁ ， C ₁ C ＝ C ₁ C ， ∴△ C ₁ BC ≌△ C ₁ DC ，

∴ C ₁ B ＝ C ₁ D . ∵ DO ＝ OB ， ∴ C ₁ O ⊥ BD ，        　

但　 AC ⊥ BD ， AC ∩ C ₁ O ＝ O ， ∴ BD ⊥ 平面 AC ₁ .

又　 C ₁ C 平面 AC ₁ ， ∴ C ₁ C ⊥ BD .               　  

（ Ⅱ ）当 ＝ 1 时，能使 A ₁ C ⊥ 平面 C ₁ BD . 

证明一： ∵ ＝ 1 ， ∴ BC ＝ CD ＝ C ₁ C ，  

又　 ∠ BCD ＝ ∠ C ₁ CB ＝ ∠ C ₁ CD .

由此可推得　 BD ＝ C ₁ B ＝ C ₁ D .

∴ 三棱锥 C － C ₁ BD 是正三棱锥 .

设　 A ₁ C 与 C ₁ O 相交

∵ A ₁ C ₁ ∥ AC ，且 A ₁ C ₁ ∶ OC ＝ 2 ∶ 1 ，

∴ C ₁ G ∶ GO ＝ 2 ∶ 1.

又　 C ₁ O 是正三角形 C ₁ BD 的 BD 边上的高和中线，

∴ 点 G 是正三角形 C ₁ BD 的中心， ∴ CG ⊥ 平面 C ₁ BD .

即　 A ₁ C ⊥ 平面 C ₁ BD .  

证明二：由（ Ⅰ ）知， BD ⊥ 平面 AC ₁ ，

∵ A ₁ C 平面 AC ₁ ，

∴ BD ⊥ A ₁ C .  

当 ＝ 1 时，平行六面体的六个面是全等的菱形，

同 BD ⊥ A ₁ C 的证法可得 BC ₁ ⊥ A ₁ C .

又　 BD ∩ BC ₁ ＝ B ，

∴ A ₁ C ⊥ 平面 C ₁ BD .