早教吧作业答案频道 -->数学-->
如图,已知:A(-2,-3),C(0,-1),B点与A点关于C点中心对称,抛物线y=ax2+bx+c过A、B两点且对称轴为x=-1.(1)求抛物线的解析式;(2)在直线AB下方的抛物线上求一点P,使△ABP的面积最
题目详情
如图,已知:A(-2,-3),C(0,-1),B点与A点关于C点中心对称,抛物线y=ax2+bx+c过A、B两点且对称轴为x=-1.
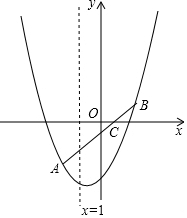
(1)求抛物线的解析式;
(2)在直线AB下方的抛物线上求一点P,使△ABP的面积最大,求出P点的坐标和△ABP面积的最大值.

(1)求抛物线的解析式;
(2)在直线AB下方的抛物线上求一点P,使△ABP的面积最大,求出P点的坐标和△ABP面积的最大值.
▼优质解答
答案和解析
 (1)∵A、B关于C中心对称,A(-2,-3),C(0,-1),
(1)∵A、B关于C中心对称,A(-2,-3),C(0,-1),
∴B(2,1),
由抛物线对称轴为x=-1,得到
,
解得:
,
则抛物线解析式为y=
x2+x-3;
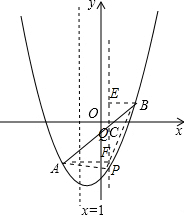
(2)过P作PQ⊥x轴,交AB于点Q,AF⊥PQ,BE⊥PQ,
设P坐标为(m,
m2+m-4),则Q(m,m-1),
∴PQ=m-1-
m2-m+4=-
m2+3,
∴S△ABP=S△APQ+S△BPQ=
PQ•AF+
PQ•BE=
PQ•(AF+BE)=
•(-
m2+3)•(2+2)=-m2+6,
∵a=-1<0,
∴S△ABP有最大值,当m=3时,S△ABP最大值为6,此时P坐标为(3,
).
 (1)∵A、B关于C中心对称,A(-2,-3),C(0,-1),
(1)∵A、B关于C中心对称,A(-2,-3),C(0,-1),∴B(2,1),
由抛物线对称轴为x=-1,得到
|
解得:
|
则抛物线解析式为y=
| 1 |
| 2 |
(2)过P作PQ⊥x轴,交AB于点Q,AF⊥PQ,BE⊥PQ,
设P坐标为(m,
| 1 |
| 2 |
∴PQ=m-1-
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABP=S△APQ+S△BPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵a=-1<0,
∴S△ABP有最大值,当m=3时,S△ABP最大值为6,此时P坐标为(3,
| 7 |
| 2 |
看了如图,已知:A(-2,-3),...的网友还看了以下:
a b是非零向量且满足(a-2b)垂直a,(b-2a)垂直b,则a与b的夹角是如题已知(a-2b) 2020-05-15 …
关于高中直线函数问题拜托各位了3Q直线x+a^2y+1=0与直线(a^2+1)x-by+3=0互相 2020-05-16 …
若向量a=(cosA,sinA),b=(cosB,sinB),a与b不共线,则a 与b一定满足A、 2020-05-16 …
设a,b,c分别是三角形ABC中角A,B,C所对的边长,则直线sinA*x+ay+c=0与bx-s 2020-05-19 …
设a,b,c分别为ΔABC中角A,B,C所对边的边长,则直线sinA*x+ay+c=0与bx*si 2020-05-19 …
设a,b,c分别是三角形ABC中角A,B,C所对的边长,则直线sinA*x+ay+c=0与bx-s 2020-05-19 …
已知向量a不等于b,|b|不等于1,对任意t属于R,恒有|a-tb|大等于|a-b|.现给出下列四 2020-05-20 …
已知下列命题:1在△ABC中∠A=∠C-∠B则△ABC为直角三角形2在△ABC中若∠A:∠B:∠C 2020-07-04 …
在平面直角坐标系中,点A,B的坐标分别是(0,1),(3,0),下列各组点中,都在以线段AB为直径 2020-07-09 …
已知在平面直角坐标系中,点A,B的坐标分别为A(3,0)B(0,4),点C的坐标为C(-2,0)点 2020-07-21 …