在直角坐标系中，已知△ABC的三个顶点是A（0，a）、B（b，0）、C（c，0），D是线段AB上任一点，直线OD交直线AC于E，∠ADO和∠ABO的平分线交于点P，若E点在AC边的延长线上，∠ACB与∠AED的平分

Question

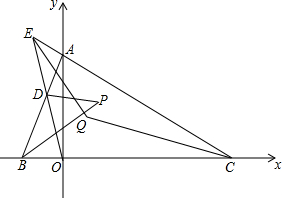
在直角坐标系中，已知△ABC的三个顶点是A（0，a）、B（b，0）、C（c，0），D是线段AB上任一点，直线OD交直线AC于E，∠ADO和∠ABO的平分线交于点P，若E点在AC边的延长线上，∠ACB与∠AED的平分线交于Q点，下面两个结论：
①∠P+∠Q的值不变；
②∠P-∠Q的值不变；
其中只有一个结论是正确的，请选择正确的结论并给出证明，求出定值．

Answer 1

①∠P+∠Q的值不变；
理由：∵∠ADO和∠ABO的平分线交于点P，
∴∠ADP=(1)/(2)∠ADO=∠ABP+∠P，∠ABP=(1)/(2)∠ABO，
∵∠ADO=∠ABO+∠BOE，
∴(1)/(2)∠ADO=(1)/(2)∠ABO+(1)/(2)∠BOE=(1)/(2)∠ABO+∠P，
∴∠P=(1)/(2)∠BOE，
∵∠ACB与∠AED的平分线交于Q点，
∴∠CEQ+∠ECQ=(1)/(2)（∠OEC+∠OCE），
∵∠BOE=∠OCE+∠OEC，
∴∠CEQ+∠ECQ=(1)/(2)∠BOE，
∴∠P=∠CEQ+∠ECQ，
∵∠Q+∠CEQ+∠ECQ=180°，
∴∠P+∠Q=180°，
∴∠P+∠Q的值不变．