早教吧作业答案频道 -->数学-->
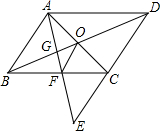
如图，E是▱ABCD的边DC延长线上的一点，且CE=DC，连接CE=DC，连接AE，分别交BC、BD于点F、G，连接AC交BD于点O，连接OF，求证：AB=2OF．
题目详情
如图，E是▱ABCD的边DC延长线上的一点，且CE=DC，连接CE=DC，连接AE，分别交BC、BD于点F、G，连接AC交BD于点O，连接OF，求证：AB=2OF．
▼优质解答
答案和解析
证明：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，AO=OC，
∵CD=CE，
∴AB=CE，∠BAF=∠CEF，
在△ABF和△ECF中，
，
∴△ABF≌△ECF，
∴BF=FC，
∵AO=OC，
∴AB=2OF．
∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，AO=OC，
∵CD=CE，
∴AB=CE，∠BAF=∠CEF，
在△ABF和△ECF中，
|
∴△ABF≌△ECF，
∴BF=FC，
∵AO=OC，
∴AB=2OF．
看了如图，E是▱ABCD的边DC延...的网友还看了以下：
平面向量a,b,e,满足|e|=1,ae=1,be=2,|a-b|=2则ab的最小值|a-b|=2 2020-04-05 …
若n阶方阵A与B满足AB+A+B=E（E为单位矩阵）.证明（1）B+E为可逆矩阵（2)(B+E)^ 2020-04-05 …
已知a+b+c=H a+b+e=J a+d+e=K b+c+d=M c+d+e=N 求a=?b=? 2020-05-16 …
设栈的初始为空,元素a,b,c,d,e,f,g依次入栈,以下出栈序列不可能出现的是A,a,b,c, 2020-05-17 …
大家看看我这个矩阵的证明哪里有问题已知A,B为n阶方阵,且B=B^2,A=B+E,证明A可逆,并求 2020-06-09 …
用以下英文宇母填在上a,a,a,a,a,a,b,e,e,d,e,e,e,e,e,e,f,g,g用以 2020-06-24 …
设矩阵A,B满足A=E(1,3)E(5(-2))BE(3,2(1/2)),则有A.B=E(1,3) 2020-06-28 …
高中函数题：设f(x)=x/e^x,a≠b,f(a)=f(b),比较a+b与2的大小我是这么想的但 2020-07-13 …
已知直角坐标系平面内点A（4,0）B(2,-2),C(1,1)在直角坐标平面内求一点P,使点A,B 2020-07-31 …
在平面直角坐标系中,已知A(-1.0)B(0.2)点C在第二象限,CD⊥x轴,垂足为D,且△CDA≌ 2021-01-22 …