早教吧作业答案频道 -->数学-->
已知Rt△ABC中,∠BAC=90°,AB=AC,△CDE的边CE在射线AC上,CE<AC,∠DCE=90°,CD=CA,沿CA方向平移△CDE,使点C移动到点A,得到△ABF,过点F作FG⊥BC,垂足为点G,连接EG,DG.(1)如图1,边CE
题目详情
已知Rt△ABC中,∠BAC=90°,AB=AC,△CDE的边CE在射线AC上,CE<AC,∠DCE=90°,CD=CA,沿CA方向平移△CDE,使点C移动到点A,得到△ABF,过点F作FG⊥BC,垂足为点G,连接EG,DG.
(1)如图1,边CE在线段AC上,求证:GC=GF;
(2)在以下A,B两题中任选一题解答,我选择___题.
A.在图1中,求证:△EFG≌△DCG;
B.如图2,边CE在线段AC的延长线上,其余条不变.
①在图2中,求证:△EFG≌△DCG;
②若∠CDE=20°,直接写出∠CGE的度数.
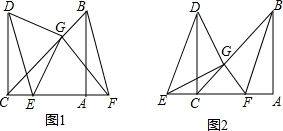
(1)如图1,边CE在线段AC上,求证:GC=GF;
(2)在以下A,B两题中任选一题解答,我选择___题.
A.在图1中,求证:△EFG≌△DCG;
B.如图2,边CE在线段AC的延长线上,其余条不变.
①在图2中,求证:△EFG≌△DCG;
②若∠CDE=20°,直接写出∠CGE的度数.

▼优质解答
答案和解析
证明:(1)如图1,
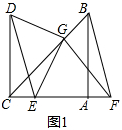
∵Rt△ABC中,∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°,
∵FG⊥CG,
∴∠FGC=90°,
∴∠GCF+∠GFC=90°,
∴∠GCF=45°=∠GCF,
∴GC=GF,
∵∠DCE=90°
∴∠DCG=90°-45°=45°
∴∠DCG=∠GCF,
∵平移△CDE,得到△ABF,
∴CA=EF,
∵CD=CA,
∴CD=EF,
在△EFG和△DCG中,
,
∴△EFG≌△DCG;
(2)①如图2,
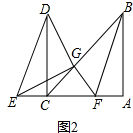
与(1)同理可证:GC=GF,∠GCF=∠GFC=45°
∵∠DCE=90°,
∴∠DCF=90°
∴∠DCG=90°-∠GCF=45°
∴∠DCG=∠GFC
∵△ABF由△CDE平移得到,
∴EC=FA
∴EF=CA
∵AC=CD
∴EF=CD
在△EFG和△DCG中,
,
∴△EFG≌△DCG.
②∠CGE=20°.

∵Rt△ABC中,∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°,
∵FG⊥CG,
∴∠FGC=90°,
∴∠GCF+∠GFC=90°,
∴∠GCF=45°=∠GCF,
∴GC=GF,
∵∠DCE=90°
∴∠DCG=90°-45°=45°
∴∠DCG=∠GCF,
∵平移△CDE,得到△ABF,
∴CA=EF,
∵CD=CA,
∴CD=EF,
在△EFG和△DCG中,
|
∴△EFG≌△DCG;
(2)①如图2,

与(1)同理可证:GC=GF,∠GCF=∠GFC=45°
∵∠DCE=90°,
∴∠DCF=90°
∴∠DCG=90°-∠GCF=45°
∴∠DCG=∠GFC
∵△ABF由△CDE平移得到,
∴EC=FA
∴EF=CA
∵AC=CD
∴EF=CD
在△EFG和△DCG中,
|
∴△EFG≌△DCG.
②∠CGE=20°.
看了已知Rt△ABC中,∠BAC=...的网友还看了以下:
把下面的式子写成(A+B)(A-B)的形式(1)(a+b+c+d)(-a-b+c+d)(2)(把下 2020-04-27 …
如图所示,数轴上点A,B,C,D分别对应有理数a,b,c,d,其中A和B关于原点对称,1化简根号下 2020-05-16 …
如图,数轴上有A、B、C、D四个点,分别对应的数为a、b、c、d,且满足a,b是方程|x+9|=1 2020-06-12 …
如图,数轴上有A、B、C、D四个点,分别对应的数为a、b、c、d,且满足a,b是方程|x+9|=1 2020-06-12 …
如图,数轴上有A、B、C、D四个点,分别对应的数为a、b、c、d,且满足a,b是方程|x+9|=1 2020-06-12 …
在评奖会上,A、B、C、D、E、F、G、H竞争一项金奖.由一个专家小组投票,票数最多的将获金奖.如 2020-06-27 …
两船质量均为M静止于湖面上,a船上站有质量为M2的人,现人以水平速度v从a跳到b船,再从b跳到a, 2020-06-27 …
设⊙O的半径为r,直线a上一点到圆心的距离为d,若d=r,则直线a与⊙O的位置关系是()(A)相交 2020-07-26 …
在△ABC中,已知AB=AC=4cm,BC=6cm,D是BC的中点,以D为圆心作一个半径为3cm的 2020-07-26 …
定义在D上的函数f(x),如果满足对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f( 2020-07-31 …