早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,过B作BE⊥AD交AD于F,交AC于E.(1)求证:△ABE为等腰三角形;(2)已知AC=11,AB=6,求BD长.
题目详情
如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,过B作BE⊥AD交AD于F,交AC于E.
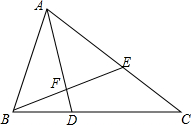
(1)求证:△ABE为等腰三角形;
(2)已知AC=11,AB=6,求BD长.

(1)求证:△ABE为等腰三角形;
(2)已知AC=11,AB=6,求BD长.
▼优质解答
答案和解析
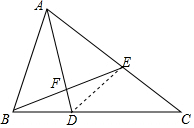 (1)证明:∵BE⊥AD,
(1)证明:∵BE⊥AD,
∴∠AFE=∠AFB=90°,
又∵AD平分∠BAC,
∴∠EAF=∠BAF,
又∵在△AEF和△ABF中
∠AFE+∠EAF+∠AEF=180°,∠AFB+∠BAF+∠ABF=180°
∴∠AEF=∠ABF,
∴AE=AB,
∴△ABE为等腰三角形;
(2) 连接DE,
∵AE=AB,AD平分∠BAC,
∴AD垂直平分BE,
∴BD=ED,
∴∠DEF=∠DBF,
∵∠AEF=∠ABF,
∴∠AED=∠ABD,
又∵∠ABC=2∠C,
∴∠AED=2∠C,
又∵△CED中,∠AED=∠C+∠EDC,
∴∠C=∠EDC,
∴EC=ED,
∴CE=BD.
∴BD=CE=AC-AE=AC-AB=11-6=5.
 (1)证明:∵BE⊥AD,
(1)证明:∵BE⊥AD,∴∠AFE=∠AFB=90°,
又∵AD平分∠BAC,
∴∠EAF=∠BAF,
又∵在△AEF和△ABF中
∠AFE+∠EAF+∠AEF=180°,∠AFB+∠BAF+∠ABF=180°
∴∠AEF=∠ABF,
∴AE=AB,
∴△ABE为等腰三角形;
(2) 连接DE,
∵AE=AB,AD平分∠BAC,
∴AD垂直平分BE,
∴BD=ED,
∴∠DEF=∠DBF,
∵∠AEF=∠ABF,
∴∠AED=∠ABD,
又∵∠ABC=2∠C,
∴∠AED=2∠C,
又∵△CED中,∠AED=∠C+∠EDC,
∴∠C=∠EDC,
∴EC=ED,
∴CE=BD.
∴BD=CE=AC-AE=AC-AB=11-6=5.
看了如图,在△ABC中,∠ABC=...的网友还看了以下:
关于刚力力学的计算题一个圆盘,半径为R,角速度为ω,在摩擦系数为μ的平面上原地转动,求到停止时,圆 2020-05-14 …
如图所示,横截面为正方形的金属棒ab静止在倾角为θ的平行导轨上,导轨上端有导线相连,垂直于导轨平面 2020-05-17 …
如图所示,倾角为θ的平行金属导轨宽度L,电阻不计,底端接有阻值为R的定值电阻,处在与导轨平面垂直向 2020-05-17 …
亮纹线宽度的计算单缝宽为a,在缝后放一焦距为f的透镜,在透镜的焦平面上放一屏幕,用波长为λ的平行光 2020-06-21 …
如图,长度为12cm、底面积为的平底玻璃试管A重为0.2N,其中放有一个重为G的铁块。把它们一起放 2020-07-20 …
如图所示,P、N是两个长为的平行板,它们相距,今有一个质量为、带电量为的正电荷以速度沿平行板面的方 2020-07-22 …
在探究杠杆平衡条件的实验中:(1)小明发现杠杆左端低右端高,要使它在水平位置平衡,应将杠杆右端的平 2020-07-29 …
如图所示,一辆长,高,质量为的平顶车,车顶面光滑,在牵引力为零时,仍在向前运动,设车运动时受到的阻 2020-08-02 …
某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4,则命中环数 2020-11-04 …
等厚干涉问题1波长为λ的平行单色光,垂直照射到劈尖薄膜上,劈尖薄膜的折射率为n,第三级亮纹对应的薄膜 2020-11-16 …