早教吧作业答案频道 -->数学-->
如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.(1)求证:△ABE≌△FCE;(2)连接AC、BF,若AE=12BC,求证:四边形ABFC为矩形;(3)在(2
题目详情
如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
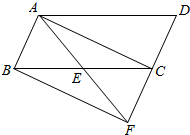
(1)求证:△ABE≌△FCE;
(2)连接AC、BF,若AE=
BC,求证:四边形ABFC为矩形;
(3)在(2)条件下,直接写出当△ABC再满足___时,四边形ABFC为正方形.

(1)求证:△ABE≌△FCE;
(2)连接AC、BF,若AE=
| 1 |
| 2 |
(3)在(2)条件下,直接写出当△ABC再满足___时,四边形ABFC为正方形.
▼优质解答
答案和解析
证明:(1)∵四边形ABCD为平行四边形,
∴AB∥DC,
∴∠ABE=∠ECF,
又∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中,
∵
,
∴△ABE≌△FCE(ASA);
(2)∵△ABE≌△FCE,
∴BE=EC,AE=EF,
∴四边形ABFC为平行四边形,
又∵AE=
BC,
∴AF=BC,
∴四边形ABFC为矩形;
(3)当△ABC为等腰三角形时,即AB=AC时,四边形ABFC为正方形;
理由如下:
∵AB=AC,E为BC的中点,
∴AE⊥BC,
∵四边形ABFC为平行四边形,
∴四边形ABFC是菱形,
又∵四边形ABFC是矩形,
∴四边形ABFC为正方形.
故答案为:AB=AC.
∴AB∥DC,
∴∠ABE=∠ECF,
又∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中,
∵
|
∴△ABE≌△FCE(ASA);

(2)∵△ABE≌△FCE,
∴BE=EC,AE=EF,
∴四边形ABFC为平行四边形,
又∵AE=
| 1 |
| 2 |
∴AF=BC,
∴四边形ABFC为矩形;
(3)当△ABC为等腰三角形时,即AB=AC时,四边形ABFC为正方形;
理由如下:
∵AB=AC,E为BC的中点,
∴AE⊥BC,
∵四边形ABFC为平行四边形,
∴四边形ABFC是菱形,
又∵四边形ABFC是矩形,
∴四边形ABFC为正方形.
故答案为:AB=AC.
看了如图,已知E是平行四边形ABC...的网友还看了以下:
设四阶矩阵B=1−101000000−101−101,C=2102000034132102,且矩阵 2020-04-12 …
设四阶矩阵A=[a1,-y2,y3,-y4],B=[b1,y2,-y3,-y4].|A|=4;B= 2020-05-17 …
将四个矩阵合并成一个矩阵A=[1,2;3,4]B=[11,22;33,44]C=[111,222; 2020-06-02 …
(2010•潍坊)学校计划用地面砖铺设教学楼前矩形广场的地面ABCD,已知矩形广场地面的长为100 2020-06-15 …
如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为EF,展平 2020-07-09 …
线性代数设A为三阶矩阵,A=(A1,A2,A3),|A|=-3.求|2A2,2A1-A2,-A3| 2020-07-09 …
矩阵A已知R(A)=2.求a.b的值该矩阵为三行四列矩阵1-1123a-1253b6 2020-07-09 …
在四边形内找一点,使该点到各边距离都相等的图形是_____20,在四边形内找一点,使该点到各边距离 2020-07-30 …
已知2个3×4的矩阵(A矩阵、B矩阵),求它们的和(C矩阵)与差(D矩阵).输出时,ABCD四个矩 2020-08-02 …
如图,用四种颜色去涂图中编号为1,2,3,4的四个矩形,使得任意两个相邻矩形颜色都不相同,则涂色方 2020-08-02 …