早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长,交DC于点F,求证:(1)△ABE≌△CFE;(2)四边形ABFD是平行四边形.
题目详情
如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长,交DC于点F,求证:
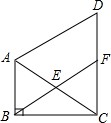
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形.

(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形.
▼优质解答
答案和解析
证明:(1)∵△ACD是等边三角形,
∴∠DCA=60°,
∵∠BAC=60°,
∴∠DCA=∠BAC,
在△ABE与△CFE中,
,
∴△ABE≌△CFE;
(2)∵E是AC的中点,
∴BE=EA,
∵∠BAE=60°,
∴△ABE是等边三角形,
∴△CEF是等边三角形,
∴∠CFE=60°,
∵△ACD是等边三角形,
∴∠CDA=∠DCA=60°,
∴∠CFE=∠CDA,
∴BF∥AD,
∵∠DCA=∠BAC=60°,
∴AB∥DC,
∴四边形ABFD是平行四边形.
∴∠DCA=60°,
∵∠BAC=60°,
∴∠DCA=∠BAC,
在△ABE与△CFE中,
|
∴△ABE≌△CFE;
(2)∵E是AC的中点,
∴BE=EA,
∵∠BAE=60°,
∴△ABE是等边三角形,
∴△CEF是等边三角形,
∴∠CFE=60°,
∵△ACD是等边三角形,
∴∠CDA=∠DCA=60°,
∴∠CFE=∠CDA,
∴BF∥AD,
∵∠DCA=∠BAC=60°,
∴AB∥DC,
∴四边形ABFD是平行四边形.
看了如图,在△ABC中,∠ABC=...的网友还看了以下:
a,b,c且a<b<c,试找出它们的共同点,并证明你的结论.a=3,b=4,c=5(3^2+4^2= 2020-03-30 …
这个等式成立吗?C(9,0)+C(9,1)+…+C(9,9)=(1+1)^9=2^9=512成立的 2020-04-07 …
2014年我省财政收入比2013年增长8.9%,2015年比2014年增长9.5%,若2013年和 2020-06-19 …
小波号军舰向敌舰发炮,已知军舰和敌舰在同一平面,炮弹经过A(0,10),B(10,9),C(5,9 2020-07-12 …
用计算器计算.c+3=c+3+5=c+3+5+7=c+3+5+7+9=c+3+5+7+9+cc=c+ 2020-10-31 …
在一次青年歌手大奖赛中,10名评委对一名歌手的评分(单位:分)如下:9.5,9.4,9.7,9.7, 2020-11-17 …
在一次青年歌手大奖赛中,10名评委对一名歌手的评分(单位:分)如下:9.5,9.4,9.7,9.7, 2020-11-17 …
在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos2C=-1/9,其中C为锐角.(1)求 2020-12-31 …
24.以下符合C语言语法的赋值表达式是()。A.a=9+b+c=d+924.以下符合C语言语法的赋值 2020-12-31 …
总体X的一组样本值为9.6、9.8、9.4,则可得总体X均值E(X)的点估计为————(A)9.4; 2020-12-31 …