早教吧作业答案频道 -->数学-->
如图,已知,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.(1)当x为何值时,PQ∥BC;(2
题目详情
如图,已知,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
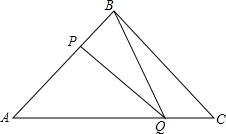
(1)当x为何值时,PQ∥BC;
(2)S△BCQ:S△ABC=1:3时,求S△BPQ:S△ABC的值;
(3)在现有条件下,哪些边对应成比例就能使△APQ与△CQB相似?并写出对应成比例的边.

(1)当x为何值时,PQ∥BC;
(2)S△BCQ:S△ABC=1:3时,求S△BPQ:S△ABC的值;
(3)在现有条件下,哪些边对应成比例就能使△APQ与△CQB相似?并写出对应成比例的边.
▼优质解答
答案和解析
(1)当PQ∥BC时,AP:AB=AQ:AC,
∵AP=4x,AQ=30-3x,
∴
=
,
解得:x=
;
即当x=
,PQ∥BC;
(2)∵S△BCQ:S△ABC=1:3
∴CQ:AC=1:3,
∴CQ=10c,
∴时间用了
秒,
∴AP=
cm,
∵由(1)知,此时PQ∥BC,
∴△APQ∽△ABC,相似比为
,
∴S△APQ:S△ABC=4:9,
∴四边形PQCB与三角形ABC面积比为5:9,即S四边形PQCB=,
S△ABC,
又∵S△BCQ:S△ABC=1:3,即S△BCQ=
S△ABC,
∴S△BPQ=S四边形PQCB-S△BCQ═
S△ABC-
S△ABC=
S△ABC,
∴S△BPQ:S△ABC=2:9=
;
(3)∵BA=BC,
∴∠A=∠C,
当AP:CQ=AQ:BC,△APQ∽△CQB;
当AQ:CQ=AP:BC,△APQ∽△CBQ;
∴对应成比例的边为
=
或
=
.
∵AP=4x,AQ=30-3x,
∴
| 4x |
| 20 |
| 30-2x |
| 30 |
解得:x=
| 10 |
| 3 |
即当x=
| 10 |
| 3 |
(2)∵S△BCQ:S△ABC=1:3
∴CQ:AC=1:3,
∴CQ=10c,
∴时间用了
| 10 |
| 3 |
∴AP=
| 40 |
| 3 |
∵由(1)知,此时PQ∥BC,
∴△APQ∽△ABC,相似比为
| 2 |
| 3 |
∴S△APQ:S△ABC=4:9,
∴四边形PQCB与三角形ABC面积比为5:9,即S四边形PQCB=,
| 5 |
| 9 |
又∵S△BCQ:S△ABC=1:3,即S△BCQ=
| 1 |
| 3 |
∴S△BPQ=S四边形PQCB-S△BCQ═
| 5 |
| 9 |
| 1 |
| 3 |
| 2 |
| 9 |
∴S△BPQ:S△ABC=2:9=
| 2 |
| 9 |
(3)∵BA=BC,
∴∠A=∠C,
当AP:CQ=AQ:BC,△APQ∽△CQB;
当AQ:CQ=AP:BC,△APQ∽△CBQ;
∴对应成比例的边为
| AP |
| CQ |
| AQ |
| BC |
| AQ |
| CQ |
| AP |
| BC |
看了如图,已知,在△ABC中,BA...的网友还看了以下:
乙看到路旁的树木在向北运动,甲看乙静止不动,若甲、乙都以地面为参照物.则它们应该是()A.甲向南、 2020-05-20 …
在Rt△ABC中,∠C=90,AC=3,BC=4,点P以一定的速度沿AC边由A向C运动,点Q以1c 2020-06-06 …
如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向 2020-07-09 …
如图,“游云西行而谓月之东驰”说的是()A.云向西飘移,就等于月亮向东运动B.月亮向东运动,就等于 2020-07-10 …
位移是可以直接相加减的吗?比如说A相对于B以10m/s向右运动.C相对于A以10m/s向右运动.但 2020-07-18 …
矩形ABCD中,AD=18cm,AB=12cm,A处有一动点E以1cm/s的速度由A向B运动,C处有 2020-11-06 …
如图:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,点P以一定的速度沿AC边由A向C运 2020-11-30 …
第三观察者如果A相对于C以0.6c的速度向东运动,B相对于C以0.6c的速度向西运动.对于C来说,A 2020-12-09 …
沙尘飞扬的方向不可以用来判断风向的参照吗下列现象不可以用来判断风向的参照是()A沙尘飞扬的方向B旗帜 2020-12-15 …
如图,在△ABC中,∠C=90°,AC=80cm,BC=60cm,动点P在线段CA上从C点出发沿CA 2021-01-16 …