早教吧作业答案频道 -->数学-->
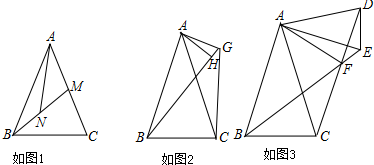
已知,等腰△ABC,AB=AC(1)如图1,BM是△ABC的中线,点N在BM上,且∠ANM=∠MBC,求证:BC=AN;(2)如图2,点G为外一点,∠BGC=∠BAC,AH⊥BG于H,若BH=7,HG=1,求线段CG的长;(3)如图3,等腰△A
题目详情
已知,等腰△ABC,AB=AC
(1)如图1,BM是△ABC的中线,点N在BM上,且∠ANM=∠MBC,求证:BC=AN;
(2)如图2,点G为外一点,∠BGC=∠BAC,AH⊥BG于H,若BH=7,HG=1,求线段CG的长;
(3)如图3,等腰△ABC和等腰△ADE共顶点A,AD=AE,顶角∠DAE=∠BAC,点F是线段BE和CD的交点,连AF,请写出∠AFC与∠ADE之间的等量关系,并证明你的结论.
(1)如图1,BM是△ABC的中线,点N在BM上,且∠ANM=∠MBC,求证:BC=AN;
(2)如图2,点G为外一点,∠BGC=∠BAC,AH⊥BG于H,若BH=7,HG=1,求线段CG的长;
(3)如图3,等腰△ABC和等腰△ADE共顶点A,AD=AE,顶角∠DAE=∠BAC,点F是线段BE和CD的交点,连AF,请写出∠AFC与∠ADE之间的等量关系,并证明你的结论.

▼优质解答
答案和解析
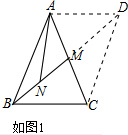 (1)如图1,延长BM至点D,使DM=BM,
(1)如图1,延长BM至点D,使DM=BM,
∵AM=CM,
∴四边形ABCD是平行四边形,
∴AD=BC,∠DBC=∠ADB,
∵∠ANM=∠DBC,
∴∠ANM=∠ADB,
∴AN=AD,
∴BC=AN;
(2)如图2,延长CG,过点A作AM⊥CG于点M,
∵AH⊥BG,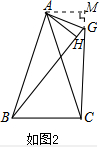
∴∠AHB=∠AMC,
∵∠BAC=∠BGC,
∴∠ABH=∠ACM,
在△CMA和△BHA中,
,
∴△CMA≌△BHA(AAS),
∴CM=BH=7,AM=AH,
在Rt△AMG和△Rt△AHG中,
,
∴△AMG≌△AHG(HL),
∴GM=GH=1,
∴CG=CM-GM=7-1=6,
(3)如图3,设AE与DF交于点M,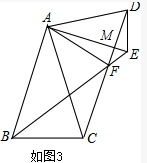
∵∠DAE=∠BAC,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴∠ABE=∠ACD,
∴A、B、C、F四点共圆,
∴∠ABC+∠AFC=180°,
∴∠ADE=∠ABC,
∴∠ADE+∠AFC=180°.
 (1)如图1,延长BM至点D,使DM=BM,
(1)如图1,延长BM至点D,使DM=BM,∵AM=CM,
∴四边形ABCD是平行四边形,
∴AD=BC,∠DBC=∠ADB,
∵∠ANM=∠DBC,
∴∠ANM=∠ADB,
∴AN=AD,
∴BC=AN;
(2)如图2,延长CG,过点A作AM⊥CG于点M,
∵AH⊥BG,

∴∠AHB=∠AMC,
∵∠BAC=∠BGC,
∴∠ABH=∠ACM,
在△CMA和△BHA中,
|
∴△CMA≌△BHA(AAS),
∴CM=BH=7,AM=AH,
在Rt△AMG和△Rt△AHG中,
|
∴△AMG≌△AHG(HL),
∴GM=GH=1,
∴CG=CM-GM=7-1=6,
(3)如图3,设AE与DF交于点M,

∵∠DAE=∠BAC,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
|
∴△ABE≌△ACD(SAS),
∴∠ABE=∠ACD,
∴A、B、C、F四点共圆,
∴∠ABC+∠AFC=180°,
∴∠ADE=∠ABC,
∴∠ADE+∠AFC=180°.
看了已知,等腰△ABC,AB=AC...的网友还看了以下:
(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求 2020-06-13 …
(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求 2020-06-15 …
(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求 2020-07-22 …
如图,在四边形ABCD中,AD∥BC,且AD<BC,AC、BD为两条对角线,且AC⊥BD,AC=B 2020-07-22 …
如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF 2020-07-29 …
如图,已知AC垂直于BC,垂足为C,且AC和BC分别为BAD和ABE的平分线,说明AD如图,已知AC 2020-11-03 …
(本题满分12分)如图1,△ABC的边BC在直线上,AC⊥BC,且AC=BC;△EFP的边FP也在直 2020-12-13 …
为了立一块广告牌,要制造一个三角形的支架,三角形支架形状如图,要求∠ACB=60°,BC的长度大于1 2020-12-20 …
为了竖一块广告牌,要制造三角形支架.三角形支架如图所示,要求∠ACB=60°,BC的长度大于1米,且 2020-12-20 …
为了立一块广告牌,要制造一个三角形的支架,三角形支架形状如图,要求∠ACB=60°,BC的长度大于1 2020-12-20 …