早教吧作业答案频道 -->数学-->
如图,AB是O的直径,DB,DC分别与O相切于B,C,OD交O于点E,(1)求证:∠AEC=∠CDO;(2)若cos∠DCE=45,求sin∠AEC的值.
题目详情
如图,AB是 O的直径,DB,DC分别与 O相切于B,C,OD交 O于点E,
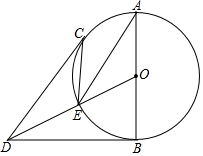
(1)求证:∠AEC=∠CDO;
(2)若cos∠DCE=
,求sin∠AEC的值.

(1)求证:∠AEC=∠CDO;
(2)若cos∠DCE=
| 4 |
| 5 |
▼优质解答
答案和解析
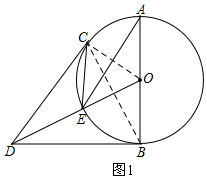 证明:(1)如图1,连接OC、BC,
证明:(1)如图1,连接OC、BC,
∵DB,DC分别与 O相切于B,C,
∴DC=BD,∠DCO=90°,
∴∠DCB+∠BCO=90°,
∵OC=OB,
∴OD是BC的中垂线,
∴∠CDO+∠DCB=90°,
∴∠BCO=∠CDO,
∵OC=OB,
∴∠BCO=∠OBC,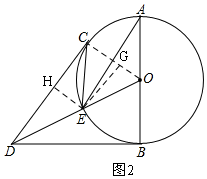
∵∠AEC=∠OBC,
∴∠AEC=∠BCO=∠CDO;
(2)如图2,连接OC,过E作EH⊥CD于H,EG⊥CO于G,
∴∠EHC=∠EGC=90°,
∵∠DCO=90°,
∴四边形HEGC是矩形,
∴EH=CG,EG=HC,
Rt△CEH中,cos∠DCE=
=
,
设CH=4x,CE=5x,则EH=3x,
∴EH=CG=3x,EG=HC=4x,
设 o的半径为r,则OE=OC=r,OG=r-3x,
由勾股定理得:r2=(4x)2+(r-3x)2,
r=
x,
∵EG∥AD,
∴∠GEO=∠CDO,
∴∠AEC=∠CDO=∠GEO,
∴sin∠AEC=sin∠CDO=sin∠GEO=
=
=
.
 证明:(1)如图1,连接OC、BC,
证明:(1)如图1,连接OC、BC,∵DB,DC分别与 O相切于B,C,
∴DC=BD,∠DCO=90°,
∴∠DCB+∠BCO=90°,
∵OC=OB,
∴OD是BC的中垂线,
∴∠CDO+∠DCB=90°,
∴∠BCO=∠CDO,
∵OC=OB,
∴∠BCO=∠OBC,

∵∠AEC=∠OBC,
∴∠AEC=∠BCO=∠CDO;
(2)如图2,连接OC,过E作EH⊥CD于H,EG⊥CO于G,
∴∠EHC=∠EGC=90°,
∵∠DCO=90°,
∴四边形HEGC是矩形,
∴EH=CG,EG=HC,
Rt△CEH中,cos∠DCE=
| 4 |
| 5 |
| CH |
| CE |
设CH=4x,CE=5x,则EH=3x,
∴EH=CG=3x,EG=HC=4x,
设 o的半径为r,则OE=OC=r,OG=r-3x,
由勾股定理得:r2=(4x)2+(r-3x)2,
r=
| 25 |
| 6 |
∵EG∥AD,
∴∠GEO=∠CDO,
∴∠AEC=∠CDO=∠GEO,
∴sin∠AEC=sin∠CDO=sin∠GEO=
| OG |
| OE |
| ||
|
| 7 |
| 25 |
看了如图,AB是O的直径,DB,D...的网友还看了以下:
A、B、C、D、E、F六种元素,其中ABCDE为短周期元素,①原子半径A<C<B<E<D②原子最外 2020-05-13 …
用这些英文字母拼词这些英文字母打乱了顺序.一个题目一个词.第一题:r,c,t,a,e,s,r第二题 2020-05-16 …
两个全等的30°、60°角的3角坂ADE和3角坂ABC如图、E A C、3点在同一直线、接BD、取 2020-05-17 …
在Windows 2000操作系统中,登陆时使用的用户名对应的密码保存的路径()。A.C:\WIND 2020-05-26 …
什么是EUR.E.A.C.Hchemicalregulations 2020-06-06 …
(1)如图①∵∠B+∠D+∠1=180°又∵∠1=∠A+∠2∠2=∠C+∠E∴∠A+∠C+∠E+∠ 2020-06-13 …
运用三角函数知识解释,为什么e=a/c越大,椭圆越扁?e=a/c越大,椭圆越圆? 2020-06-27 …
初三的数学题1.两个全等的含30°,60°角的三角形板ADE和三角形板ABC如图所示放置,E,A, 2020-07-22 …
该地质演化过程的正确排序是()A.d-e-g-f-b-a-h-cB.d-g-e-a-c-h-b-fC 2020-11-04 …
已知五种元素的原子序数的大小顺序为C>A>D>E,A,C同周期,B,C同主族.A与B形成离子化合物是 2020-11-18 …