早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,O为原点,点A的坐标为(-4,0),点B的坐标为(0,4),点C、D分别为OA、OB的中点,若正方形OCED绕点O顺时针旋转,得正方形OC′E′D′.记旋转角为a(0°<a&l
题目详情
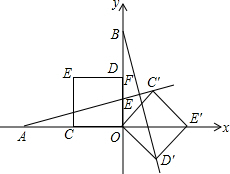
如图,在平面直角坐标系中,O为原点,点A的坐标为(-4,0),点B的坐标为(0,4),点C、D分别为OA、OB的中点,若正方形OCED绕点O顺时针旋转,得正方形OC′E′D′.记旋转角为a(0°<a<360°),连结AC′、BD′,设直线AC′与直线BD′相交于点F,则点F的纵坐标的最大值为___.

▼优质解答
答案和解析
如图,
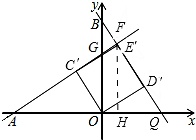
∵∠AOB=∠D′OC′,
∴∠ACO′=∠BOD′,
在△AOC′和△BOD′中,
,
∴△AOC′≌△BOD′,
∴∠OAF=∠OBF,
∵∠AGO=∠BOF
∴∠BFA=∠BOA=90°,
∴点F、B、A、O四点共圆,
∴当点F在劣弧上运动时,点F的纵坐标随∠FAO的增大而增大,
∵OC′=2,
∴点C′在以点O为圆心,2为半径的圆O上运动,
∴当AF与 O相切时,∠C′AO(即∠FAO)最大,
此时∠AC′O=90°,点E′与点F重合,点F的纵坐标达到最大.
过点F作FH⊥x轴,垂足为H,如图所示.
∵∠AC′O=90°,C′O=2,AO=4,
∴∠E′AO=30°,AC′=2
.
∴AF=2
+2.
∵∠AHF=90°,∠FAH=30°,
∴FH=
AF=
×(2
+2)=
+1.
∴点P的纵坐标的最大值为
+1.

∵∠AOB=∠D′OC′,
∴∠ACO′=∠BOD′,
在△AOC′和△BOD′中,
|
∴△AOC′≌△BOD′,
∴∠OAF=∠OBF,
∵∠AGO=∠BOF
∴∠BFA=∠BOA=90°,
∴点F、B、A、O四点共圆,
∴当点F在劣弧上运动时,点F的纵坐标随∠FAO的增大而增大,
∵OC′=2,
∴点C′在以点O为圆心,2为半径的圆O上运动,
∴当AF与 O相切时,∠C′AO(即∠FAO)最大,
此时∠AC′O=90°,点E′与点F重合,点F的纵坐标达到最大.
过点F作FH⊥x轴,垂足为H,如图所示.
∵∠AC′O=90°,C′O=2,AO=4,
∴∠E′AO=30°,AC′=2
| 3 |
∴AF=2
| 3 |
∵∠AHF=90°,∠FAH=30°,
∴FH=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴点P的纵坐标的最大值为
| 3 |
看了如图,在平面直角坐标系中,O为...的网友还看了以下:
点A的坐标为(2,3)则它关于x轴对称的点B的坐标为关于y轴对称的点C的坐标为关于原点轴对称的点D 2020-06-14 …
1:直线y=二分之一-4与x轴的交点坐标为,与y轴的交点坐标为?2:对于1:直线y=二分之一-4与 2020-06-14 …
:全站仪我假定测站坐标为x0.0;y0.0.后视定向坐标在正北方前10米是不是...:全站仪我假定 2020-06-22 …
如图所示的xOy坐标系中,y轴右侧空间存在范围足够大的匀强磁场,磁感应强度大小为B,方向垂直于xO 2020-07-25 …
平面直角坐标系内,O为原点,已知正方形OABC,若点A的坐标为(3,4),则点B的坐标为什么?我等 2020-07-30 …
已知圆的参数方程为(为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆的极坐标方程为. 2020-07-31 …
如图,点A的坐标为(2,-1),点B的坐标为(3,0),(1)在y轴的左恻,以点O为位似中心,按比 2020-08-02 …
若某点坐标为(-1,3),将坐标系顺时针旋转90°,而此点不动,则此点坐标变为.若某点坐标为(-1, 2020-12-25 …
若一个圆的圆心C坐标为(3,4),半径是5,那么坐标原点在圆?RT△ABC中,∠C=90°,AC=7 2021-01-13 …
已知圆的参数方程为(为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆的极坐标方程为. 2021-02-10 …