早教吧作业答案频道 -->数学-->
如图,在正方形ABCD中,以BC为直径的正方形内,作半圆O,AE切半圆于点F交CD于E.(1)求证:AO⊥EO.(2)连接DF,求tan∠FDE的值.
题目详情
如图,在正方形ABCD中,以BC为直径的正方形内,作半圆O,AE切半圆于点F交CD于E.
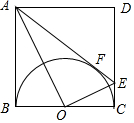
(1)求证:AO⊥EO.
(2)连接DF,求tan∠FDE的值.

(1)求证:AO⊥EO.
(2)连接DF,求tan∠FDE的值.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD为正方形,
∴∠B=∠C=90°,AB∥CD,
∴AB和CD为 O的切线,
∵AE切半圆于点F,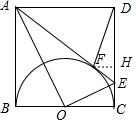
∴OA平分∠BAE,OE平分∠AEC,
而AB∥CD,
∴∠BAE+∠AEC=180°,
∴∠OAE+∠OEA=90°,
∴∠AOE=90°,
∴OA⊥OE;
(2) 作FH⊥CD于H,如图,设正方形ABCD的边长为4a,
则AF=AB=4a,OB=OC=2a,
∵∠AOE=90°,
∴∠AOB+∠COE=90°,
∵∠AOB+∠OAB=90°,
∴∠OAB=∠EOC,
∴Rt△ABO∽Rt△OCE,
∴AB:OC=OB:CE,即4a:2a=2a:CE,解得CE=a,
∴EF=EC=a,
∴EA=5a,ED=3a,
∵FH∥AD,
∴△EFH∽△EAD,
∴
=
=
,即
=
=
,
∴FH=
a,EH=
a,
∴DH=3a-
a=
a,
∴tan∠FDE=
=
=
.
∴∠B=∠C=90°,AB∥CD,
∴AB和CD为 O的切线,
∵AE切半圆于点F,

∴OA平分∠BAE,OE平分∠AEC,
而AB∥CD,
∴∠BAE+∠AEC=180°,
∴∠OAE+∠OEA=90°,
∴∠AOE=90°,
∴OA⊥OE;
(2) 作FH⊥CD于H,如图,设正方形ABCD的边长为4a,
则AF=AB=4a,OB=OC=2a,
∵∠AOE=90°,
∴∠AOB+∠COE=90°,
∵∠AOB+∠OAB=90°,
∴∠OAB=∠EOC,
∴Rt△ABO∽Rt△OCE,
∴AB:OC=OB:CE,即4a:2a=2a:CE,解得CE=a,
∴EF=EC=a,
∴EA=5a,ED=3a,
∵FH∥AD,
∴△EFH∽△EAD,
∴
| FH |
| AD |
| EF |
| EA |
| EH |
| ED |
| FH |
| 5a |
| a |
| 4a |
| EH |
| 3a |
∴FH=
| 5 |
| 4 |
| 3 |
| 4 |
∴DH=3a-
| 3 |
| 4 |
| 9 |
| 4 |
∴tan∠FDE=
| FH |
| DH |
| ||
|
| 5 |
| 9 |
看了如图,在正方形ABCD中,以B...的网友还看了以下:
一点小数学问题1.⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=3/4,则弦AC的长为多少?2 2020-03-30 …
跟三角形四心有关的题,急啊三角形ABC的内心为I,外心为O,其内切圆半径为r,外接圆半径为R,连结 2020-05-16 …
关于病句的种类及其修改方法1.内容重复2.语序不当3.搭配不当4.关联词搭配问题5.分类不当6.前 2020-07-24 …
已知圆O和圆O上的一点A1作圆O的内接正方形ABCD和内接正六边形AEFCGH2在1题所做的图中, 2020-07-26 …
1圆O的半径为R求圆O的内接正方形,圆O的外切正方形的边长比AB;AB'和面积比S内;S外2圆O的 2020-07-29 …
急求)三角形ABC内接于圆O,BC=4,S三角形ABC=6根号3,角B为锐角三角形ABC内接于圆O 2020-07-30 …
三角形ABC内接于圆O,BC=4,S三角形ABC=6被根号3,角B为锐角...三角形ABC内接于圆 2020-07-31 …
如图1、2、3、……n、M、N分别是圆O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、 2020-08-03 …
球方法《亲爱的爸爸/妈妈,我想对你说》怎么写?球做出简介、方法1.内容真实,感情真挚,立意新颖,见解 2020-11-02 …
尺规作图:已知O及O上一点A,如图.(1)求作:O的内接正方形ABCD;(保留作图痕迹,不写作法)( 2020-11-06 …