早教吧作业答案频道 -->数学-->
解决问题时需要思考:是否解决过与其类似的问题.小明从问题1解题思路中获得启发从而解决了问题2.问题1:如图①,在正方形ABCD中,E、F是BC、CD上两点,∠EAF=45°.求证:∠AEF=∠AEB.
题目详情
解决问题时需要思考:是否解决过与其类似的问题.小明从问题1解题思路中获得启发从而解决了问题2.
问题1:如图①,在正方形ABCD中,E、F是BC、CD上两点,∠EAF=45°.
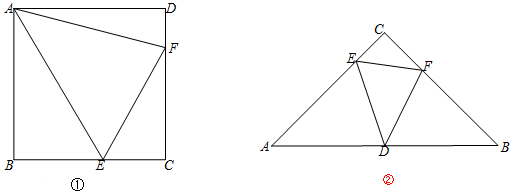
求证:∠AEF=∠AEB.
小明给出的思路为:延长EB到H,满足BH=DF,连接AH.请完善小明的证明过程.
问题2:如图②,在等腰直角△ABC中,∠ACB=90°,AC=BC=4,D为AB中点,E、F是AC、BC边上两点,∠EDF=45°.
(1)求点D到EF的距离.
(2)若AE=a,则S△DEF=___(用含字母a的代数式表示).
问题1:如图①,在正方形ABCD中,E、F是BC、CD上两点,∠EAF=45°.
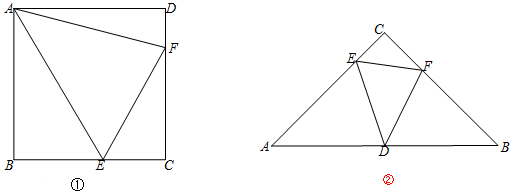
求证:∠AEF=∠AEB.
小明给出的思路为:延长EB到H,满足BH=DF,连接AH.请完善小明的证明过程.
问题2:如图②,在等腰直角△ABC中,∠ACB=90°,AC=BC=4,D为AB中点,E、F是AC、BC边上两点,∠EDF=45°.
(1)求点D到EF的距离.
(2)若AE=a,则S△DEF=___(用含字母a的代数式表示).
▼优质解答
答案和解析
问题1:证明:如图①中,延长EB到H,满足BH=DF,连接AH
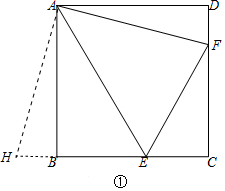
∵AB=AD,∠ABH=∠D=90°,BH=DF,
∴△ADF≌ABH,
∴∠DAF=∠BAH,AF=AH,
∵∠DAF+∠BAE=∠BAD-∠EAF=90°-45°=45°,
即∠EAH=∠BAH+∠BAE=45°,
∴∠EAH=∠EAF,
又∵AF=AH,AE=AE,
∴△AHE≌△AFE,
∴∠AEF=∠AEB.
问题2: (1)过点D分别向AC、BC、EF作垂线,垂足分别为G、H、M,
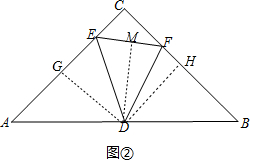
∵∠ACB=90°,∴CGDH为矩形,∵AC=BC=4,D为AB中点,
∴DG=DH=
BC=2,
∴四边形CGDH为正方形,
由问题1知∠DEG=∠DEM,
∴DM=DG=2.
(2)在Rt△DEG中,DE=
=
=
,
∵S△AED=
•AE•DG=a,
∵△DEF∽△AED,
∴
=(
)2=
,
∴S△DEF=
.
故答案为
.

∵AB=AD,∠ABH=∠D=90°,BH=DF,
∴△ADF≌ABH,
∴∠DAF=∠BAH,AF=AH,
∵∠DAF+∠BAE=∠BAD-∠EAF=90°-45°=45°,
即∠EAH=∠BAH+∠BAE=45°,
∴∠EAH=∠EAF,
又∵AF=AH,AE=AE,
∴△AHE≌△AFE,
∴∠AEF=∠AEB.
问题2: (1)过点D分别向AC、BC、EF作垂线,垂足分别为G、H、M,

∵∠ACB=90°,∴CGDH为矩形,∵AC=BC=4,D为AB中点,
∴DG=DH=
| 1 |
| 2 |
∴四边形CGDH为正方形,
由问题1知∠DEG=∠DEM,
∴DM=DG=2.
(2)在Rt△DEG中,DE=
| EG2+DG2 |
| (a-2)2+22 |
| a2-4a+8 |
∵S△AED=
| 1 |
| 2 |
∵△DEF∽△AED,
∴
| S△DEF |
| S△AED |
| DE |
| AE |
| a2-4a+8 |
| a2 |
∴S△DEF=
| a2-4a+8 |
| a |
故答案为
| a2-4a+8 |
| a |
看了解决问题时需要思考:是否解决过...的网友还看了以下:
关于卡文迪许扭秤实验对物理学的贡献,下列说法中正确的是()A.发现了万有引力的存在B.解决了微小距 2020-06-16 …
中英文摘要,跪求翻译本次设计研究的这套髓内钉机器人锁钉器,是针对目前医院内做锁钉手术的弊端和缺点, 2020-06-26 …
管理学概论作业1单选题1.为正确决策奠定坚实的基础。A.信息系统B.智囊系统C.决策系统D.分析系 2020-07-06 …
2016年3月14日,十一届全国人大五次会议表决通过了《刑事诉讼法修正案》.据此回答第23--24 2020-07-23 …
2015年8月24日召开的十二届全国人大常委会第十六次会议表决通过了刑法修正案(九)、新修订的大气污 2020-11-06 …
“一次不公正的司法判决比多次不公正的其他举动为祸尤烈。因为这些不公正的举动不过弄脏水流,而不公正的判 2020-11-07 …
宗教工作是党和国家工作中的重要组成部分。“民族、宗教无小事”,对此理解正确的是()A.能否正确认识和 2020-11-11 …
关于遵义会议的评价,正确的是().A.中国共产党从幼稚走向成熟的历史转折点B.中国共产党的历史上一个 2020-11-13 …
下列描述不正确的是()A.决策树法综合考虑了每一种结果B.决策树法计算简便,鲜明易懂C.风险型决策的 2020-11-27 …
今年2月,在联合国安理会上,中俄两国投反对票,否决了叙利亚问题决议草案,维护了世界正义。我国可以行使 2020-12-09 …