早教吧作业答案频道 -->数学-->
如图1:在平面直角坐标系内,O为坐标原点,线段AB两端点在坐标轴上且点A(-4,0)点B(0,3),将AB向右平移4个单位长度至OC的位置(1)直接写出点C的坐标;(2)如图2,过点C作CD⊥x轴
题目详情
如图1:在平面直角坐标系内,O为坐标原点,线段AB两端点在坐标轴上且点A(-4,0)点B(0,3),将AB向右平移4个单位长度至OC的位置
(1)直接写出点C的坐标___;
(2)如图2,过点C作CD⊥x轴于点D,在x轴正半轴有一点E(1,0),过点E作x轴的垂线,在垂线上有一动点P,求三角形PCD的面积;
(3)如图3,在(2)的条件下,连接AC,当△ACP的面积为
时,求点P的坐标.
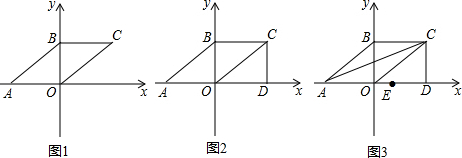
(1)直接写出点C的坐标___;
(2)如图2,过点C作CD⊥x轴于点D,在x轴正半轴有一点E(1,0),过点E作x轴的垂线,在垂线上有一动点P,求三角形PCD的面积;
(3)如图3,在(2)的条件下,连接AC,当△ACP的面积为
| 33 |
| 2 |

▼优质解答
答案和解析
(1)∵B(0,3),将AB向右平移4个单位长度至OC的位置,
∴C(4,3),
故答案为:(4,3);
(2)∵CD⊥x轴于点D,
∴CD=3,即h=3,OD=4,
∵E(1,0),
∴DE=3,
∴S△PCD=
×3×3=
;
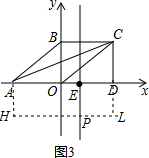 (3)①设P1(1,y),
(3)①设P1(1,y),
∴S△ACP=S四边形PEDC+S△AEP-S△ADC
=
+
-
=
,
∴y=6,
∴P1(1,6)
②设P2(1,-a),如图3,过P作PL∥AD交CD的延长线于L,过A作AH⊥PL于H,
∴S△ACP=S四边形AHLC-S△AHP-S△LCP
=
-
-
=
,
∴a=
∴P2(1,-
),
综上所述:P(1,6),(1,-
).
∴C(4,3),
故答案为:(4,3);
(2)∵CD⊥x轴于点D,
∴CD=3,即h=3,OD=4,
∵E(1,0),
∴DE=3,
∴S△PCD=
| 1 |
| 2 |
| 9 |
| 2 |
 (3)①设P1(1,y),
(3)①设P1(1,y),∴S△ACP=S四边形PEDC+S△AEP-S△ADC
=
| 3(3+y) |
| 2 |
| 5y |
| 2 |
| 8×3 |
| 2 |
| 33 |
| 2 |
∴y=6,
∴P1(1,6)
②设P2(1,-a),如图3,过P作PL∥AD交CD的延长线于L,过A作AH⊥PL于H,
∴S△ACP=S四边形AHLC-S△AHP-S△LCP
=
| 8(2a+3) |
| 2 |
| 5a |
| 2 |
| 3(a+3) |
| 2 |
| 33 |
| 2 |
∴a=
| 9 |
| 4 |
∴P2(1,-
| 9 |
| 4 |
综上所述:P(1,6),(1,-
| 9 |
| 4 |
看了如图1:在平面直角坐标系内,O...的网友还看了以下:
若向量a×向量b=0,则向量a=0向量或向量b=0向量 2020-04-05 …
已知A(-1,0),B(1,0),点P满足向量PA·向量PB=0,则|向量PA+向量PB|等于(要 2020-04-12 …
已知常数a>0,向量c=(0,a),i=(1,0),经过原点O以c+λi为方向向量的直线与经过定点 2020-05-13 …
若向量a×向量b=0,则向量a=0向量或向量b=0向量 2020-05-15 …
给出平面上4个点O(0,0),A(3,0),B(0,3),C(sina,cosa),(1)若向量A 2020-05-16 …
切向加速度为0,法向加速度为0 质点做什么运动 切向加速度为0,法向加速度不切向加速度为0,法向加 2020-05-17 …
已知常数a>0,向量c=(0,a),i=(1,0),经过原点O以c+λi为方向向量的直线与经过定点 2020-06-12 …
1、设A(0,1),B(2,4),C(-3,-1),且向量AB=向量CD,求点D坐标2、设向量a= 2020-07-18 …
二维数组里面a[0+2]是指向行还是列*(a[0+2]+2)是不是等于a[2][2]a[0]就是指 2020-07-29 …
什么叫向量配成顶点式y=(x-1)^2-4顶点(1,-4)点(1,-4)绕点(3,0)顺时针逆时针 2020-08-01 …