早教吧作业答案频道 -->数学-->
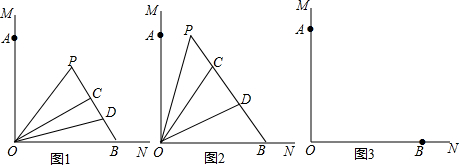
如图1,已知∠MON=90°,点A、B分别是∠MON的边OM,ON上的点.且OA=OB=1,将线段OA绕点O顺时针旋转α(0°<α<180°)得到线段OC,∠AOC的角平分线OP与直线BC相交于点P,点D是线段BC的中点
题目详情
如图1,已知∠MON=90°,点A、B分别是∠MON的边OM,ON上的点.且OA=OB=1,将线段OA绕点O顺时针旋转α(0°<α<180°)得到线段OC,∠AOC的角平分线OP与直线BC相交于点P,点D是线段BC的中点,连接OD.
(1)若α=30°,如图2,∠P的度数为___°;
(2)若0°<α<90°,如图1,求∠P的度数;
(3)在下面的A、B两题中任选一题解答.
A:在(2)的条件下,在图1中连接PA,求PA2+PB2的值.
B:如图3,若90°<α<180°,其余条件都不变.请在图3中画出相应的图形,探究下列问题:①直接写出此时∠P的度数;②求此时PC2+PB2的值.
我选择___题.
(1)若α=30°,如图2,∠P的度数为___°;
(2)若0°<α<90°,如图1,求∠P的度数;

(3)在下面的A、B两题中任选一题解答.
A:在(2)的条件下,在图1中连接PA,求PA2+PB2的值.
B:如图3,若90°<α<180°,其余条件都不变.请在图3中画出相应的图形,探究下列问题:①直接写出此时∠P的度数;②求此时PC2+PB2的值.
我选择___题.
▼优质解答
答案和解析
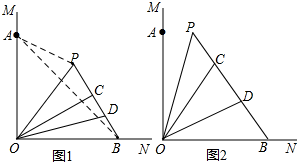 (1)如图2,若α=30°,则∠COP=
(1)如图2,若α=30°,则∠COP=
∠AOC=15°,∠BOC=60°,
∵CO=AO=BO,
∴△BOC是等边三角形,
∴∠OCB=60°,
∴∠P的度数为:60°-15°=45°,
故答案为:45°;
(2)证明:由旋转得,OA=OC,∠AOC=α,
∵OA=OB,
∴OC=OB,
∵点D是线段BC的中点,
∴OD⊥BC,∠COD=∠BOD=
∠BOC,
∵∠AOB=90°,
∴∠COD=
(90°-α),
∵OP平分∠AOC,
∴∠POC=
α,
∴∠POD=∠POC+∠COD=45°,
∵∠ODP=90°,
∴∠P=90°-45°=45°;
(3)选择A题.
如图1,连接AB、AP,
∵OP平分∠AOC,
∴∠AOP=∠COP,
在△AOP和△COP中,
,
∴△AOP≌△COP(SAS),
∴∠APO=∠CPO=45°,
∴∠APB=90°,
∴在Rt△APB中,由勾股定理得,PA2+PB2=AB2,
∵在Rt△AOB中,由勾股定理得,AB2=OA2+OB2=12+12=2,
∴PA2+PB2=2.
选择B题.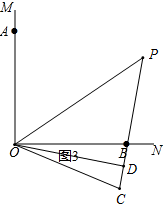
①∠P=45°.
理由:如图3,根据旋转可得,OC=OA=OB,
∵D是BC中点,
∴OD⊥BC,即∠ODP=90°,
且OD平分∠BOC,
又∵OP平分∠AOC,
∴∠DOP=∠COP-∠COD=
∠AOC-
∠BOC=
∠AOB=
×90°=45°,
∴Rt△ODP中,∠P=45°;
②PC2+PB2的值为2.
理由:∵OD⊥BC,∠P=45°,
∴△OPD是等腰直角三角形,
∴PD=OD,
∵PC=PD+BD,PB=PD-BD,
∴PC2+PB2
=(PD+BD)2+(PD-BD)2
=2PD2+2BD2
=2(PD2+BD2)
=2(OD2+BD2)
=2×OB2
=2×12
=2
故PC2+PB2的值为2.
 (1)如图2,若α=30°,则∠COP=
(1)如图2,若α=30°,则∠COP=| 1 |
| 2 |
∵CO=AO=BO,
∴△BOC是等边三角形,
∴∠OCB=60°,
∴∠P的度数为:60°-15°=45°,
故答案为:45°;
(2)证明:由旋转得,OA=OC,∠AOC=α,
∵OA=OB,
∴OC=OB,
∵点D是线段BC的中点,
∴OD⊥BC,∠COD=∠BOD=
| 1 |
| 2 |
∵∠AOB=90°,
∴∠COD=
| 1 |
| 2 |
∵OP平分∠AOC,
∴∠POC=
| 1 |
| 2 |
∴∠POD=∠POC+∠COD=45°,
∵∠ODP=90°,
∴∠P=90°-45°=45°;
(3)选择A题.
如图1,连接AB、AP,
∵OP平分∠AOC,
∴∠AOP=∠COP,
在△AOP和△COP中,
|
∴△AOP≌△COP(SAS),
∴∠APO=∠CPO=45°,
∴∠APB=90°,
∴在Rt△APB中,由勾股定理得,PA2+PB2=AB2,
∵在Rt△AOB中,由勾股定理得,AB2=OA2+OB2=12+12=2,
∴PA2+PB2=2.
选择B题.

①∠P=45°.
理由:如图3,根据旋转可得,OC=OA=OB,
∵D是BC中点,
∴OD⊥BC,即∠ODP=90°,
且OD平分∠BOC,
又∵OP平分∠AOC,
∴∠DOP=∠COP-∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Rt△ODP中,∠P=45°;
②PC2+PB2的值为2.
理由:∵OD⊥BC,∠P=45°,
∴△OPD是等腰直角三角形,
∴PD=OD,
∵PC=PD+BD,PB=PD-BD,
∴PC2+PB2
=(PD+BD)2+(PD-BD)2
=2PD2+2BD2
=2(PD2+BD2)
=2(OD2+BD2)
=2×OB2
=2×12
=2
故PC2+PB2的值为2.
看了如图1,已知∠MON=90°,...的网友还看了以下:
已知点A(3,-4)与点B(-1,2),点P在直线AB上,且PA的膜长等于2倍PB的膜长,求点P的 2020-04-12 …
已知点A(3,-4)点B(-1,2),点P在支线AB上,且PA的膜长等于2倍PB的膜长,求点P的坐 2020-04-12 …
(1)如果把向北的方向规定为正,那么走3.5千米,走-1.2千米,走0千米的意义各是什么?(2)一 2020-04-13 …
数学题11506达人进啊已知二次函数y=-(x-h)^2+k图像的顶点P在x轴上,且他的图像经过点 2020-05-13 …
气象小组观察测得七月二十一日凌晨2时的气温是18度,上午8时的气温是21度,下午2时的气温是34度 2020-05-15 …
对下列物理量的估测,最接近实际的是()A.潜水员在水面下5米深处时面部护眼镜上所受的压力大约50N 2020-05-16 …
1.汽车上坡时的速度为28千米每时期下坡的速度为35千米每时,去时下坡的路程比上坡的路程的2倍少1 2020-05-17 …
上升过程最后1s内位移的大小一定等于下降过程中最初1s内位移的大小错误的原因?是不是因为上抛时的初 2020-05-19 …
平直公路有甲、乙两辆汽车,甲以0.5米每二次方秒的加速度由静止开始行驶,乙在甲的前方200米处以5 2020-05-22 …
一物块从粗糙斜面底端,以某一初速度开始向上滑行,到达某位置后又沿斜面下滑到底端,则物块在此运动过程 2020-06-05 …