早教吧作业答案频道 -->数学-->
如图,点B(4,4)在双曲线y=kx(x>0)上,点C在双曲线y=-6x(x<0)上,点A是x轴上一动点,连接BC、AC、AB.(1)求k的值;(2)如图1,当BC∥x轴时,△ABC的面积;(3)如图2,当点A运动到
题目详情
如图,点B(4,4)在双曲线y=
(x>0)上,点C在双曲线y=-
(x<0)上,点A是x轴上一动点,连接BC、AC、AB.
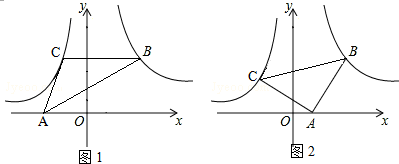
(1)求k的值;
(2)如图1,当BC∥x轴时,△ABC的面积;
(3)如图2,当点A运动到x轴正半轴时,如△ABC是等腰直角三角形,∠BAC=90°,求点A的坐标.
| k |
| x |
| 6 |
| x |

(1)求k的值;
(2)如图1,当BC∥x轴时,△ABC的面积;
(3)如图2,当点A运动到x轴正半轴时,如△ABC是等腰直角三角形,∠BAC=90°,求点A的坐标.
▼优质解答
答案和解析
(1)∵B(4,4)在双曲线y=
(x>0)上,
∴k=4×4=16;
(2)∵BC∥x轴,
∴B与C纵坐标相同,
把y=4代入y=-
中,得:x=-
,即C(-
,4),
∴BC=4+
=
,
则S△ABC=
•BC•yB纵坐标=11;
(3)过点B、C作x轴的垂线,垂足为M、N,
∵△ABC为等腰直角三角形,
∴∠CAB=90°,AC=BC,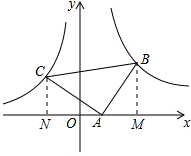
∴∠ACN+∠CAN=90°,∠BAM+∠CAN=90°,
∴∠ACN=∠BAM,
在△ABM和△CAN中,
∵
,
∴△ABM≌△CAN(AAS),
∴AN=MB=4,CN=AM,
设OA=a,则有ON=AN-OA=4-a,CN=AM=OM-OA=4-a,
∴C(a-4,4-a)(a<4),
把C坐标代入y=-
中,得:-(4-a)2=-6,
解得:a=4-
.
则点A的坐标为(4-
,0).
| k |
| x |
∴k=4×4=16;
(2)∵BC∥x轴,
∴B与C纵坐标相同,
把y=4代入y=-
| 6 |
| x |
| 3 |
| 2 |
| 3 |
| 2 |
∴BC=4+
| 3 |
| 2 |
| 11 |
| 2 |
则S△ABC=
| 1 |
| 2 |
(3)过点B、C作x轴的垂线,垂足为M、N,
∵△ABC为等腰直角三角形,
∴∠CAB=90°,AC=BC,

∴∠ACN+∠CAN=90°,∠BAM+∠CAN=90°,
∴∠ACN=∠BAM,
在△ABM和△CAN中,
∵
|
∴△ABM≌△CAN(AAS),
∴AN=MB=4,CN=AM,
设OA=a,则有ON=AN-OA=4-a,CN=AM=OM-OA=4-a,
∴C(a-4,4-a)(a<4),
把C坐标代入y=-
| 6 |
| x |
解得:a=4-
| 6 |
则点A的坐标为(4-
| 6 |
看了如图,点B(4,4)在双曲线y...的网友还看了以下:
(1)如图1,在l上找一点P,使PA+PB最小.(2)如图2,在l上找一点P,使PA+PB最小.( 2020-05-13 …
如图,如图,Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,点P是在边AB上的一个动点, 2020-05-14 …
如图,在平面直角坐标系中,直线l:y=-4/3x+4分别交x轴、y轴于点A,B,将△AOB绕点如图 2020-05-16 …
如图,在平面直角坐标系中,直线y=4/3x+4分别交x轴 y轴于AB两点,点C为OB的中点如图,在 2020-05-16 …
在华为T系列(V100R005)存储阵列设备中,创建LUN的时候,进入高级选项,预取策略有以下如图4 2020-05-31 …
如图4,点E,F分别是在等边△ABC的BC,CA边上,且BE=CF,AE,BF交于点D,求证:∠A 2020-06-06 …
如图,已知直线y=kx+b经过A(4,0)和B(0,4)两点,它与抛物线y=36/49x²交于P点 2020-06-14 …
(1)如图1,在l上找一点P,使PA+PB最小.(2)如图2,在l上找一点P,使PA+PB最小.( 2020-07-08 …
如图表示一个正比例函数与一个一次函数的图象,它们交于点a(4,3),一次函数的图象与如图表示一个正 2020-08-03 …
如图,点B(4,4)在双曲线y=kx(x>0)上,点C在双曲线y=-6x(x<0)上,点A是x轴上一 2020-11-01 …