早教吧作业答案频道 -->物理-->
如图(a),O、N、P为直角三角形的三个顶点,∠NOP=37°,OP中点处固定一电量为q1=2.0×10-8C的正点电荷,M点固定一轻质弹簧.MN是一光滑绝缘杆,其中ON长为a(a=1m),杆上穿有一带正电的小球
题目详情
如图(a),O、N、P为直角三角形的三个顶点,∠NOP=37°,OP中点处固定一电量为q1=2.0×10-8C的正点电荷,M点固定一轻质弹簧.MN是一光滑绝缘杆,其中ON长为a(a=1m),杆上穿有一带正电的小球(可视为点电荷),将弹簧压缩到O点由静止释放,小球离开弹簧后到达N点的速度为零.沿ON方向建立坐标轴(取O点处x=0),图(b)中Ⅰ和Ⅱ图线分别为小球的重力势能和电势能随位置坐标x变化的图象,其中E0=1.24×10-3J,E1=1.92×10-3J,E2=6.2×10-4J,k=9.0×109N•m2/C2,取sin37°=0.6,cos37°=0.8,g=10m/s2.
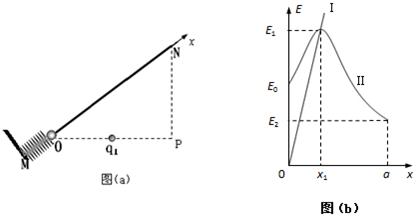
(1)求电势能为E1时小球的位置坐标x1和小球的质量m;
(2)已知在x1处时小球与杆间的弹力恰好为零,求小球的电量q2;
(3)求小球释放瞬间弹簧的弹性势能Ep.

(1)求电势能为E1时小球的位置坐标x1和小球的质量m;
(2)已知在x1处时小球与杆间的弹力恰好为零,求小球的电量q2;
(3)求小球释放瞬间弹簧的弹性势能Ep.
▼优质解答
答案和解析
(1)x1=acos37°•
•cos37°=0.32a=0.32m
x1处重力势能E1=mgx1sin37°
m=
=1×10-3kg
(2)k
=mgcos37°,其中r=x1tan37°=0.24a
带入数据,得q2=
=2.56×10-6C
(3)根据能量守恒,mga sin37°+E2-E0=EP
带入数据,得EP=5.38×10-3J
答:(1)求电势能为E1时小球的位置坐标x1为0.32m,小球的质量m1×10-3kg;
(2)已知在x1处时小球与杆间的弹力恰好为零,小球的电量q2为2.56×10-6C;
(3)求小球释放瞬间弹簧的弹性势能Ep为 5.38×10-3J
(1)x1=acos37°•
| 1 |
| 2 |
x1处重力势能E1=mgx1sin37°
m=
| E1 |
| gx1sin370 |
(2)k
| q1q2 |
| r2 |
带入数据,得q2=
| 6E1a |
| 25kq1 |
(3)根据能量守恒,mga sin37°+E2-E0=EP
带入数据,得EP=5.38×10-3J
答:(1)求电势能为E1时小球的位置坐标x1为0.32m,小球的质量m1×10-3kg;
(2)已知在x1处时小球与杆间的弹力恰好为零,小球的电量q2为2.56×10-6C;
(3)求小球释放瞬间弹簧的弹性势能Ep为 5.38×10-3J
看了如图(a),O、N、P为直角三...的网友还看了以下:
数列{a(n)}中,a(n)=2n²-bn+12(N属于正整数)是单调递增数列,求b的取值范围 2020-04-26 …
在△ABC中,a=n²,b=n²-1/2,c=n²+1/2其中n为正奇数 求证此三角形为直角三角形 2020-05-17 …
已知(a^n·b^m·b)^3=a^19·b^15,那么m、n的值分别是?3Q题中a^n指的是a的 2020-06-03 …
问一道高一数学题目编写一个程序计算s=a+aa+aaa+aaaa+……+aa…a(例如2+22+2 2020-07-19 …
编写一个程序,计算s=a+aa+aaa+.......+aa.....a(如2+22+222+22 2020-07-19 …
编写一个程序,计算s=a+aa+aaa+aaaa+…+aa…a(例如2+22+222+2222+2 2020-07-24 …
判断以下对应是否为从集合A到B的映射,并说明理由.(1)A={平面内的圆},B={平面内的三角形} 2020-07-30 …
已知等差数列{An}中,A(n+1)>An,A1A10=160,A3+A8=371)求数列{An}的 2020-10-31 …
3相电的问题有3条火线分别为A.B.C和一跟零线N用万能表测量有以下情况:A-B\A-C\B-C任意 2020-11-07 …
如何形象地理解排列公式A(n,m)=n*(n-1)*.(n-m+1)?公式中A(n,m)=n*(n- 2020-12-24 …