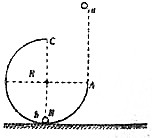
如图所示，半径为R的四分之三光滑圆轨道竖直放置，CB是竖直直径，A点与圆心等高，有小球b静止在轨道底部，小球a自轨道上方某一高度处由静止释放自A点与轨道相切进入竖直圆轨道，a，b

Question

如图所示，半径为R的四分之三光滑圆轨道竖直放置，CB是竖直直径，A点与圆心等高，有小球b静止在轨道底部，小球a自轨道上方某一高度处由静止释放自A点与轨道相切进入竖直圆轨道，a，b小球直径相等、质量之比为3：1．两小球在轨道底部发生弹性正碰，后小球b经过c点水平抛出落在离C点水平距离为2√(2)R的地面上，重力加速度为g，小球均可视为质点，求

（1）小球b碰后瞬间的速度；
（2）小球a碰后在轨道中能上升的最大高度．

Answer 1

（1）小球b离开C点后做平抛运动，则有
   2R=(1)/(2)gt2，2√(2)R=v_Ct
解得 v_C=√(2gR)
b球从B到C，由机械能守恒得：2mgR+(1)/(2)m

v

2 C

=(1)/(2)m

v

2 b

解得小球b碰后瞬间的速度 v_b=√(6gR)
（2）设两球碰撞前a球的速度为v₀．
取向左为正方向，对于两球的碰撞过程，由动量守恒和机械能守恒得：
   m_av₀=m_av_a+m_bv_b；
  (1)/(2)ma

v

2 0

=(1)/(2)ma

v

2 a

+(1)/(2)mb

v

2 b

又 m_a=3m_b；
解得 v_a=(1)/(3)v_b=(√(6gR))/(3)
设小球a碰后在轨道中能上升的最大高度为h，由机械能守恒得
  m_agh=(1)/(2)ma

v

2 a

解得  h=(1)/(3)R
答：
（1）小球b碰后瞬间的速度是√(6gR)；
（2）小球a碰后在轨道中能上升的最大高度是

作业帮用户 2017-03-04 举报

举报该用户的提问

举报类型（必填）

• 色情低俗

• 辱骂攻击

• 侮辱英烈

• 垃圾广告

• 不良流行文化

• 骗取采纳

• 其他

举报理由（必填）

0/100

提交

问题解析

（1）小球b离开C点后做平抛运动，由高度和水平位移可求出小球b经过C点时的速度，由机械能守恒求小球b碰后瞬间的速度．
（2）根据弹性碰撞遵守的规律：动量守恒和机械能守恒，列式求出碰后a球的速度，再由机械能守恒求小球a碰后在轨道中能上升的最大高度．

名师点评

本题考点：

机械能守恒定律 向心力

考点点评：

解决本题的关键要掌握弹性碰撞所遵守的规律：系统的动量守恒和机械能守恒，再结合机械能守恒、动量守恒和平抛运动的规律解答．

扫描下载二维码

©2019 作业帮 联系方式：[e-mail]  作业帮协议