早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.(1)当F为BE中点时,求证:AM=CE;(2)若ABBC=EFBF=2,求ANND的值.
题目详情
如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
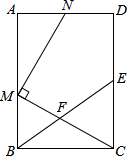
(1)当F为BE中点时,求证:AM=CE;
(2)若
=
=2,求
的值.

(1)当F为BE中点时,求证:AM=CE;
(2)若
| AB |
| BC |
| EF |
| BF |
| AN |
| ND |
▼优质解答
答案和解析
(1)当F为BE中点时,如图1,
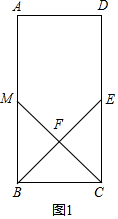
则有BF=EF.
∵四边形ABCD是矩形,
∴AB=DC,AB∥DC,
∴∠MBF=∠CEF,∠BMF=∠ECF.
在△BMF和△ECF中,
∵
,
∴△BMF≌△ECF,
∴BM=EC.
∵E为CD的中点,
∴EC=
DC,
∴BM=EC=
DC=
AB,
∴AM=BM=EC;
(2)如图2所示:设MB=a,
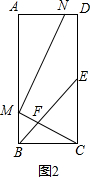
∵四边形ABCD是矩形,
∴AD=BC,AB=DC,∠A=∠ABC=∠BCD=90°,AB∥DC,
∴△ECF∽△BMF,
∴
=
=2,
∴EC=2a,
∴AB=CD=2CE=4a,AM=AB-MB=3a.
∵
=2,
∴BC=AD=2a.
∵MN⊥MC,
∴∠CMN=90°,
∴∠AMN+∠BMC=90°.
∵∠A=90°,
∴∠ANM+∠AMN=90°,
∴∠BMC=∠ANM,
∴△AMN∽△BCM,
∴
=
,
∴
=
,
∴AN=
a,ND=AD-AN=2a-
a=
a,
∴
=
=3.

则有BF=EF.
∵四边形ABCD是矩形,
∴AB=DC,AB∥DC,
∴∠MBF=∠CEF,∠BMF=∠ECF.
在△BMF和△ECF中,
∵
|
∴△BMF≌△ECF,
∴BM=EC.
∵E为CD的中点,
∴EC=
| 1 |
| 2 |
∴BM=EC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AM=BM=EC;
(2)如图2所示:设MB=a,

∵四边形ABCD是矩形,
∴AD=BC,AB=DC,∠A=∠ABC=∠BCD=90°,AB∥DC,
∴△ECF∽△BMF,
∴
| EC |
| BM |
| EF |
| BF |
∴EC=2a,
∴AB=CD=2CE=4a,AM=AB-MB=3a.
∵
| AB |
| BC |
∴BC=AD=2a.
∵MN⊥MC,
∴∠CMN=90°,
∴∠AMN+∠BMC=90°.
∵∠A=90°,
∴∠ANM+∠AMN=90°,
∴∠BMC=∠ANM,
∴△AMN∽△BCM,
∴
| AN |
| BM |
| AM |
| BC |
∴
| AN |
| a |
| 3a |
| 2a |
∴AN=
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴
| AN |
| ND |
| ||
|
看了如图,在矩形ABCD中,E为C...的网友还看了以下:
已知P(1,1)和直线2X+Y-4=0.(1)求直线M过点P且L平行于M的方程(2)若直线N过点P 2020-04-26 …
根据下列条件,求相应的等差数列{an}的有关未知数:(1)a1=20,an=54,Sn=999,求 2020-04-27 …
高一数学题求等差数列{an}的有关未知数⑴.a1=20,an=54,Sn=999,求d及n;⑵.a 2020-04-27 …
(2004•广州一模)已知曲线x2+2y2+4x+4y+4=0按向量a=(2,1)平移后得到曲线C 2020-05-15 …
根据下列条件,求相应的等差数列{an}的有关未知数:(1)a1=20,an=54,Sn=999.求 2020-07-16 …
对于RSA算法,已知e=31,n=3599,求d.由n=3599,可知pq=59*61=3599, 2020-07-17 …
根据下列条件,求相应的等差列{an}的有关未知数:(1)a1=20,an=54,Sn=999,求d 2020-07-21 …
关于比例选段的题,已知mn=ab,将它改写成比例式,使n放在第四比例项是已知a=5m,b=5cm, 2020-08-03 …
多边形对角线数为D,与数N,求D与N的关系? 2020-11-18 …
圆锥曲线提问已知动点P到点A(-2,0)与点B(2,0)的斜率之积为-1/4,点P的轨迹为曲线C1. 2021-01-11 …