早教吧作业答案频道 -->数学-->
正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.(1)证明:△ABM∽△MCN;(2)若△ABM的周长与△MCN周长之比是4:3,求NC的长;(3)设BM=x,当M点运
题目详情
正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
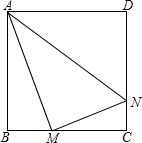
(1)证明:△ABM∽△MCN;
(2)若△ABM的周长与△MCN周长之比是4:3,求NC的长;
(3)设BM=x,当M点运动到什么位置时△ABM∽△AMN,求x的值.

(1)证明:△ABM∽△MCN;
(2)若△ABM的周长与△MCN周长之比是4:3,求NC的长;
(3)设BM=x,当M点运动到什么位置时△ABM∽△AMN,求x的值.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是正方形,
∴AB=BC=CD=4,∠B=∠C=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠CMN+∠AMB=90°.
在Rt△ABM中,∠MAB+∠AMB=90°,
∴∠CMN=∠MAB,∴∠AMN=90°,
∴∠CMN+∠AMB=90°.
在Rt△ABM中,∠MAB+∠AMB=90°,
∴∠CMN=∠MAB,
∴Rt△ABM∽Rt△MCN.
(2)∵△ABM∽△MCN,△ABM的周长与△MCN周长之比是4:3,
∴
=
=
,
∴
=
,
∴MC=3,
∴BM=4-3=1,
∴
=
,
∴NC=
(3) ∵∠B=∠AMN=90°,
∴要使△ABM∽△AMN,则有
=
,
由(1)知
=
,
∴
=
,
∴BM=MC,
∴当点M运动到BC的中点时,△ABM∽△AMN,此时,x=2.
∴AB=BC=CD=4,∠B=∠C=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠CMN+∠AMB=90°.
在Rt△ABM中,∠MAB+∠AMB=90°,
∴∠CMN=∠MAB,∴∠AMN=90°,
∴∠CMN+∠AMB=90°.
在Rt△ABM中,∠MAB+∠AMB=90°,
∴∠CMN=∠MAB,
∴Rt△ABM∽Rt△MCN.
(2)∵△ABM∽△MCN,△ABM的周长与△MCN周长之比是4:3,
∴
| BM |
| NC |
| AB |
| MC |
| 4 |
| 3 |
∴
| 4 |
| MC |
| 4 |
| 3 |
∴MC=3,
∴BM=4-3=1,
∴
| 1 |
| NC |
| 4 |
| 3 |
∴NC=
| 3 |
| 4 |
(3) ∵∠B=∠AMN=90°,
∴要使△ABM∽△AMN,则有
| AM |
| MN |
| AB |
| BM |
由(1)知
| AM |
| MN |
| AB |
| MC |
∴
| AB |
| BM |
| AB |
| MC |
∴BM=MC,
∴当点M运动到BC的中点时,△ABM∽△AMN,此时,x=2.
看了正方形ABCD边长为4,M,N...的网友还看了以下:
如果−12−x是二次根式,那么x应满足的条件是()A.x≠2的实数B.x<2的实数C.x>2的实数 2020-05-14 …
(2014•崇明县一模)如图显示了人体内能源物质的代谢途径,大写字母代表物质,其中物质Z直接参与了 2020-05-17 …
下列命题正确的是()A.若函数f(x)在x=a处连续,则函数f(x)在x=a的邻域内连续B.若函数 2020-06-12 …
如图所示,真空中有两个点电荷Q1=+4.0×10-8C和Q2=-1.0×10-8C,分别固定在x坐 2020-06-14 …
读下面漫画《民主》。下列评论不正确的是[]A.当官就是为民“做主”B.左边x长站在了人民的对立面C 2020-06-16 …
如图代表肌细胞与环境的物质交换关系。X、Y、Z表示三种细胞外液,下列叙述错误的是()A.若饮食过咸 2020-07-11 …
在平面直角坐标系中,下列说法错误的是()A.点A(-1,-3)在第四象限内\x05B.若x<0,y 2020-07-30 …
在如图所示的直角坐标中,x轴的上方存在与x轴正方向成45°角斜向右下方的匀强电场,场强的大小为E= 2020-07-31 …
若多项式x2+x10=a0+a1(x+1)+a2(x+1)2+…+a9(x+1)9+a10(x+1) 2020-10-31 …
工业上采用隔膜法电解槽电解饱和食盐水,其原理如图(X,Y为电机)(1)下列有关判断错误的是A.X的电 2020-11-02 …