早教吧作业答案频道 -->数学-->
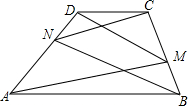
如图,梯形ABCD中AB∥CD,AB>CD,N、M分别是腰AD、CB上的点,已知∠DAM=∠CBN.求证:∠DMA=∠CNB.
题目详情
如图,梯形ABCD中AB∥CD,AB>CD,N、M分别是腰AD、CB上的点,已知∠DAM=∠CBN.求证:∠DMA=∠CNB.

▼优质解答
答案和解析
证明:连接MN,如图所示: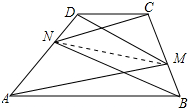
∵∠DAM=∠CBN,
∴A,B,M,N四点共圆,
∴∠DAB=∠CMN,∠ANB=∠AMB,
又∵AB∥DC,
∴∠DAB+∠ADC=180°,
∴∠CMN+∠ADC=180°.
∴C,D,N,M四点共圆,
∴∠CMD=∠DNC,
∴180°-∠DNC-∠ANB=180°-∠CMD-∠AMB,
∴∠DMA=∠CNB.

∵∠DAM=∠CBN,
∴A,B,M,N四点共圆,
∴∠DAB=∠CMN,∠ANB=∠AMB,
又∵AB∥DC,
∴∠DAB+∠ADC=180°,
∴∠CMN+∠ADC=180°.
∴C,D,N,M四点共圆,
∴∠CMD=∠DNC,
∴180°-∠DNC-∠ANB=180°-∠CMD-∠AMB,
∴∠DMA=∠CNB.
看了如图,梯形ABCD中AB∥CD...的网友还看了以下:
已知a是3个正数a.b.c中最大的数,且a/b=c/d,则a+d于c+d的大小关系是?(则a+d于c 2020-03-31 …
已知A与(B或C)=D,能否得出结论:Aand非(B与C)=非D?已知定理:A与(B或C)=D如: 2020-04-06 …
已知a+b+c=H a+b+e=J a+d+e=K b+c+d=M c+d+e=N 求a=?b=? 2020-05-16 …
在直角坐标系中,已知点A(-2.0),B(0,4)C(0.3).过C作直线交X轴于D.使以D.O. 2020-06-02 …
①若a\b=b\c=c\d=d\a,求a-b+c-d\a+b-c+d.②已知x,y,z互不相等,且 2020-06-05 …
已知函数f(x)=|log3x|,0<x<313x2−103x+8,x≥3,若存在实数a,b,c, 2020-06-12 …
如果你完成上述题目觉得正确无误后,可考虑解决以下问题,注意:本题不计入总分.两个正方形如图放置,其 2020-06-13 …
(2014•浦东新区二模)(文)定义区间(c,d),[c,d),(c,d],[c,d]的长度均为d 2020-06-29 …
(2014•浦东新区二模)(理)定义区间(c,d),[c,d),(c,d],[c,d]的长度均为d 2020-06-29 …
1、△ABC∽△A'B'C',BD和B'D'是它们的对应中线,已知AC比A'C'=3比2,B'D' 2020-08-01 …