早教吧作业答案频道 -->数学-->
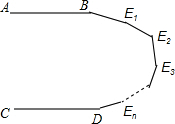
如图,直线AB∥CD,E1,E2…En是两直线间的n个点,那么∠B+∠E1+∠E2+…+∠En+∠D=度(用含n的代数式表示)
题目详情
如图,直线AB∥CD,E1,E2…En是两直线间的n个点,那么∠B+∠E1+∠E2+…+∠En+∠D=___度(用含n的代数式表示)

▼优质解答
答案和解析
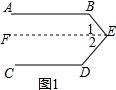 如图1,过E作EF∥AB,则EF∥CD,
如图1,过E作EF∥AB,则EF∥CD,
∴∠B+∠1=180°①,
∠D+∠1=180°②,
①+②得∠B+∠1+∠D+∠2=360°,
即∠B+∠D+∠E=360°,
分别过E1,E2作E1F∥AB,E2G∥AB,则E1F∥E2G∥CD,如图2,
∴∠1+∠B=∠2+∠3=∠4+∠D=180°,
∴∠1+∠B+∠2+∠3+∠4+∠D=540°=3×180°,
所以可得:拐点的个数n与角的和之间的关系是(n+1)•180°,
∴∠B+∠E1+∠E2+∠E3+…+∠En-1+∠D=(n+1-1)•180°=n180°,
故答案为:180n
 如图1,过E作EF∥AB,则EF∥CD,
如图1,过E作EF∥AB,则EF∥CD,∴∠B+∠1=180°①,
∠D+∠1=180°②,
①+②得∠B+∠1+∠D+∠2=360°,
即∠B+∠D+∠E=360°,
分别过E1,E2作E1F∥AB,E2G∥AB,则E1F∥E2G∥CD,如图2,

∴∠1+∠B=∠2+∠3=∠4+∠D=180°,
∴∠1+∠B+∠2+∠3+∠4+∠D=540°=3×180°,
所以可得:拐点的个数n与角的和之间的关系是(n+1)•180°,
∴∠B+∠E1+∠E2+∠E3+…+∠En-1+∠D=(n+1-1)•180°=n180°,
故答案为:180n
看了如图,直线AB∥CD,E1,E...的网友还看了以下:
如图,在x轴上有两点A(m,0),B(n,0)(n>m>0).分别过点A,点B作x轴的垂线,交抛物 2020-05-14 …
已知直线m,n相交于点B,点A,C分别为直线m,n上的点,AB=BC=1,且∠ABC=60°,点E 2020-06-19 …
32个罗经点每个点怎么读出来?罗经中的32个罗经点(N.N/E.NNE.NE/N.NE.NE/EE 2020-06-19 …
请问下面的经纬度数分别是哪些城市?107°E,6°S.96°E,17°N.90°E,23.5°N. 2020-07-03 …
下列各城市中,一年有两次阳光直射现象的是()A、悉尼(151°E,32°S)B、纽约(74°W,4 2020-07-18 …
一架飞机从北京(116°E,40°N)起飞,沿着116°E经线一直向北或向南飞行,最后能不能回到北 2020-07-18 …
求证e^i(4π/n)+e^i(8π/n)+...+e^i4(n-1)π/n+e^i(4nπ/n)= 2020-11-01 …
下列城市中,一年有两次阳光直射现象的是()A.海口(110°E,20°N)B.汕头(116°E,23 2020-11-12 …
用C++求不超过30000E数列的最大E数的值/*数列:E(1)=E(2)=1E(n)=(n-1)* 2020-11-20 …
limn→+00,e的n分之1次方*(1-e)除以n*(1-e的n分之1次方)=e-1是怎么算来的? 2020-12-17 …