如图，Rt△ABC中，∠C=90°，∠ABC=30°，AC=2，△ABC绕点C顺时针旋转得△A1B1C，当A1落在AB边上时，连接B1B，取BB1的中点D，连接A1D，则A1D的长度是（）A.7B.2C.3D.22

Question

如图，Rt△ABC中，∠C=90°，∠ABC=30°，AC=2，△ABC绕点C顺时针旋转得△A₁B₁C，当A₁落在AB边上时，连接B₁B，取BB₁的中点D，连接A₁D，则A₁D的长度是（　　）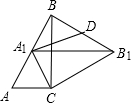

A.

√(7)

B. 2

C. 3

D. 2

√(2)

Answer 1

∵∠C=90°，∠ABC=30°，AC=2，
∴AB=4，∠A=60°，
由勾股定理得，BC=√(AB2-AC2)=2√(3)，
由旋转的性质可知，CA=CA′，由∠A=60°，
∴△ACA′是等边三角形，
∴AA′=2，
∴A′B=2，
由旋转的性质可知，△B₁BC是等边三角形，
∴BB₁=2√(3)，
∴BD=√(3)，
由勾股定理得，A₁D=√(7)
故选：A．