早教吧作业答案频道 -->数学-->
在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,点M在AB1的中点,点P为对角线AC1上的动点,点Q为底面ABCD上的动点(P,Q可以重合),则MP+PQ的最小值是.
题目详情
在长方体ABCD-A1B1C1D1中,AB=
,BC=AA1=1,点M在AB1的中点,点P为对角线AC1上的动点,点Q为底面ABCD上的动点(P,Q可以重合),则MP+PQ的最小值是___.
| | 2 |
▼优质解答
答案和解析
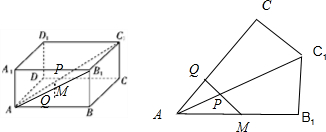 由题意,要求MP+PQ的最小值,就是P到底面ABCD的距离的最小值与MP的最小值之和,Q是P在底面上的射影距离最小,展开三角形ACC1与三角形AB1C1,在同一个平面上,
由题意,要求MP+PQ的最小值,就是P到底面ABCD的距离的最小值与MP的最小值之和,Q是P在底面上的射影距离最小,展开三角形ACC1与三角形AB1C1,在同一个平面上,
如图,易知∠B1AC1=∠C1AC=30°,AM=
,可知MQ⊥AC时,MP+PQ的最小,最小值为:
sin60°=
.
故答案为
.
 由题意,要求MP+PQ的最小值,就是P到底面ABCD的距离的最小值与MP的最小值之和,Q是P在底面上的射影距离最小,展开三角形ACC1与三角形AB1C1,在同一个平面上,
由题意,要求MP+PQ的最小值,就是P到底面ABCD的距离的最小值与MP的最小值之和,Q是P在底面上的射影距离最小,展开三角形ACC1与三角形AB1C1,在同一个平面上,如图,易知∠B1AC1=∠C1AC=30°,AM=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 4 |
故答案为
| 3 |
| 4 |
看了在长方体ABCD-A1B1C1...的网友还看了以下:
一个整式与多项式x的平方减y的平方的差为x的平方加y的平方,则这个整式为()一个整式与多项式x的平 2020-04-22 …
用三连格(横的或竖的)去框右面表格中的数,每次框三个数.是11~70之间.(1)框出的三个数的和最 2020-05-13 …
我真的可以坦然的面对他吗?曾经很喜欢他,在乎他的一切。可是,在知道他有喜欢的人之后,我不知道该怎么 2020-05-13 …
不同时期具有突出成就的中国古典文学形式,都有许多著名的代表作。对下列材料的表述,正确的是①它的体裁 2020-05-13 …
设椭圆的中心在原点,长轴在x轴上,离心率e=根号3/2.已知点P(0,3/2)到这个椭圆上的点的最 2020-05-16 …
海豚表演时的讲解词谁能告诉我怎么简单的写啊主要是精辟的开场白和优美的中间的句子大家看过海豚表演吧就 2020-05-16 …
在探究“影响滑动摩擦力大小的因素”的实验中.(1)为了探究滑动摩擦力与速度大小的关系 在不同速度下 2020-05-16 …
《我身上裹着的是我的父母》阅读答案北极,被称为世界的冰窖.在这儿,生活着一种浑身长满绒毛的鸟儿—— 2020-05-16 …
如图(1)正方形ABCD中,以A为顶点做角PAQ=45度,AP,AQ分别交直线BC,CD于E,F( 2020-05-20 …
1.长为2a的线段AB的两个端点A和B分别在x轴和y轴上滑动,求线段AB的中点的轨迹方程.2.已知 2020-05-22 …