早教吧作业答案频道 -->数学-->
对于一个三边长为p,q,r的三角形,其中p≤q≤r,称函数y=px2-rx+q为这个三角形的“派生函数”,或称这个函数是由这个三角形“派生”出的.(1)一个三角形的边长为3,4,5,请直接写出
题目详情
对于一个三边长为p,q,r的三角形,其中p≤q≤r,称函数y=px2-rx+q为这个三角形的“派生函数”,或称这个函数是由这个三角形“派生”出的.
(1)一个三角形的边长为3,4,5,请直接写出这个三角形的派生函数___.
(2)如图1,△ABC中,AB=AC,
①如图1,∠A>60°,则BC是△ABC的最长边,求证:△ABC的派生函数与x轴没有公共点;
②如图2,∠A<60°,则BC使△ABC的最短边,若△ABC的派生函数与x轴有公共点,求cosC的范围;
③如图3,∠A=60°,记△ABC的派生函数为C1.:y=ax2-bx+c.C1的图象顶点为A,与y轴相交于B,直线AB交x轴于点C,C2是三角形△BOC的派生函数,若C2,C1恰有一个公共点,请直接写出a的取值范围___.
(1)一个三角形的边长为3,4,5,请直接写出这个三角形的派生函数___.
(2)如图1,△ABC中,AB=AC,
①如图1,∠A>60°,则BC是△ABC的最长边,求证:△ABC的派生函数与x轴没有公共点;
②如图2,∠A<60°,则BC使△ABC的最短边,若△ABC的派生函数与x轴有公共点,求cosC的范围;
③如图3,∠A=60°,记△ABC的派生函数为C1.:y=ax2-bx+c.C1的图象顶点为A,与y轴相交于B,直线AB交x轴于点C,C2是三角形△BOC的派生函数,若C2,C1恰有一个公共点,请直接写出a的取值范围___.

▼优质解答
答案和解析
(1) 根据“派生函数”的定义可知,三角形的边长为3,4,5,
这个三角形的派生函数为y=3x2-5x+4.
故答案为y=3x2-5x+4.
(2)①证明:如图1中,设AB=AC=m,BC=n,
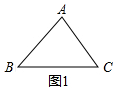
∵∠A=60°,
∴m=mn,
∴△ABC的派生函数为y=mx2-nx+m,
∵△=n2-4m2=(n+2m)(n-2m),
∵n+2m>0,n-2m<0,
∴△<0,
∴△ABC的派生函数与x轴没有公共点.
② 如图2中,作AH⊥BC于H.设AB=AC=m,BC=n,n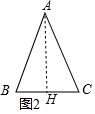
∴△ABC的派生函数为y=nx2-mx+m,
∵△ABC的派生函数与x轴有公共点,
∴△≥0,
∴m2-4mn≥0,
∵m>0,
∴m≥4n,
∵AB=AC,AH⊥BC,
∴BH=HC=
n,
∴cosC=
=
=
,
当m=4n时,cosC=
,
∴0<cosC≤
.
③如图3中,
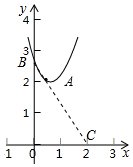
∵∠A=60°,AB=AC,
∴△ABC是等边三角形,设边长为a,
∴△ABC的派生函数C1为y=ax2-ax+a,
∴点B(0,a),顶点A(
,
a),
∴直线AB的解析式为y=-
ax+a,
∴点C(2,0),
∴OB=a,OC=2,BC=
,
a、当0<a≤2时,△BOC的派生函数C2为y=ax2-
x+2,
易知函数C1与C2恰有一个公共点,请直接写出a的取值范围,
b、当a>2时,△BOC的派生函数C2为y=2x2-
x-a,
易知函数C1与C2有两个交点,不符合题意,
∴当C1与C2恰有一个公共点时a的取值范围:0<a≤2.
故答案为0<a≤2.
这个三角形的派生函数为y=3x2-5x+4.
故答案为y=3x2-5x+4.
(2)①证明:如图1中,设AB=AC=m,BC=n,

∵∠A=60°,
∴m=m
∴△ABC的派生函数为y=mx2-nx+m,
∵△=n2-4m2=(n+2m)(n-2m),
∵n+2m>0,n-2m<0,
∴△<0,
∴△ABC的派生函数与x轴没有公共点.
② 如图2中,作AH⊥BC于H.设AB=AC=m,BC=n,n

∴△ABC的派生函数为y=nx2-mx+m,
∵△ABC的派生函数与x轴有公共点,
∴△≥0,
∴m2-4mn≥0,
∵m>0,
∴m≥4n,
∵AB=AC,AH⊥BC,
∴BH=HC=
| 1 |
| 2 |
∴cosC=
| HC |
| AC |
| ||
| m |
| n |
| 2m |
当m=4n时,cosC=
| 1 |
| 8 |
∴0<cosC≤
| 1 |
| 8 |
③如图3中,

∵∠A=60°,AB=AC,
∴△ABC是等边三角形,设边长为a,
∴△ABC的派生函数C1为y=ax2-ax+a,
∴点B(0,a),顶点A(
| 1 |
| 2 |
| 3 |
| 4 |
∴直线AB的解析式为y=-
| 1 |
| 2 |
∴点C(2,0),
∴OB=a,OC=2,BC=
| 4+a2 |
a、当0<a≤2时,△BOC的派生函数C2为y=ax2-
| a2+4 |
易知函数C1与C2恰有一个公共点,请直接写出a的取值范围,
b、当a>2时,△BOC的派生函数C2为y=2x2-
| a2+4 |
易知函数C1与C2有两个交点,不符合题意,
∴当C1与C2恰有一个公共点时a的取值范围:0<a≤2.
故答案为0<a≤2.
看了 对于一个三边长为p,q,r的...的网友还看了以下:
有一堆苹果,十个十个数剩九个,九个九个数剩八个,八个八个数剩七个,七个七个数剩六个,六个六个数剩五 2020-04-06 …
算术有几个乒乓球啊?头好晕啊!一个箱子里装有乒乓球,2个一组拿剩1个3个一组拿剩1个,4个一组拿剩 2020-05-13 …
(若兮)(后面接个两个字的词、大家觉得该接什么呢?)很温暖又很伤感的词,很简单也很顺嘴.前提是在, 2020-06-03 …
求各种答案:Strings=newString("xyz")究竟创建了几个StringObject 2020-06-04 …
有五个人和一个猴子在一个荒岛上吃椰子为生.一次他们采了很多椰子后沉沉的睡了.第一个人半夜醒了把椰子 2020-06-21 …
有五个人和一个猴子在一个荒岛上吃椰子为生.一次他们采了很多椰子后沉沉的睡了.第一个人半夜醒了把椰子 2020-06-21 …
一箱石榴,如果5个5个地数,最后还多1个,如果3个3个地数,最后也多一个,如果七个七个地数,最后一 2020-07-07 …
有1箱鸡蛋,2个2个得数多1个,3个3个的数多1个,4个4个的数多1个,5个5个的数多1个,6个6个 2020-11-17 …
数学问题有一盘水果,3个3个地数余2个,4个4个数余3,5个5个数余4个,问这个盘子里最少有多少个水 2020-11-19 …
200912月的英语六级估分,快速阅读:6个4个仔细阅读:6个《阅读做的太差了》听力短对话:6个听力 2020-12-05 …