早教吧作业答案频道 -->数学-->
已知函数f(x)=2-|x|,x≤2(x-2)2,x>2,若方程f(x)+f(2-x)=t恰有4个不同的实数根,则实数t
题目详情
已知函数f(x)=
,若方程f(x)+f(2-x)=t恰有4个不同的实数根,则实数t的取值范围是___.
| |
|
▼优质解答
答案和解析
由f(x)=
,
得f(2-x)=
,
g(x)=f(x)+f(2-x)=
画出函数g(x)的图象(如图),f(-
)=f(
)=
.
方程f(x)+f(2-x)=t恰有4个不同的实数根,则实数t的取值范围是:(
,2)
故答案为:(
,2)
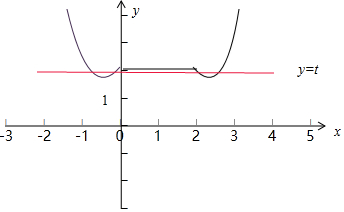
|
得f(2-x)=
|
g(x)=f(x)+f(2-x)=
|
画出函数g(x)的图象(如图),f(-
| 1 |
| 2 |
| 5 |
| 2 |
| 7 |
| 4 |
方程f(x)+f(2-x)=t恰有4个不同的实数根,则实数t的取值范围是:(
| 7 |
| 4 |
故答案为:(
| 7 |
| 4 |

看了已知函数f(x)=2-|x|,...的网友还看了以下:
简单对数函数已知2^a=5^b=10,则1/a+1/b=?(为什么是1?怎么算?) 2020-03-30 …
据汪之成的《上海俄侨史》统计:从1904年到1917年,上海公共租界的俄侨人数大体稳定在360人左 2020-04-07 …
找出等量关系.并列方成解答.一个数减去6后,扩大7倍等于这个数的2倍,求这个数.已知△-□=2.8 2020-05-13 …
甲乙两个同学解方程x的平方+px+q=0,甲看错了一次项的系数,得根2和7,乙看错了常数项,得根1 2020-05-16 …
一个小球以10米/秒的速度在平坦的地面上开始滚动,并且均匀减速,滚动20米后小球停下来.问:小球滚 2020-06-30 …
求数列根2,根号下2加根2,根号下2加根号下2加根2.的极限 2020-07-13 …
甲和乙同学解方程x²+px+q=0,甲看错了一次项的系数,得根2和7,乙看错了常数项,得根1和-1 2020-08-01 …
一元二次方程应用题甲乙两同学解方程x^2+px+q=0,甲看错了一次项系数,得根2和7,乙看错了常 2020-08-01 …
对于实数x、y规定一个新运算“x△y=ax+by(a、b是常数)”,已知2△3=11,5△(-3)= 2020-11-01 …
已知啊a,b互为相反数,c,d互为倒数,e为非零整数,求根2﹙a+b﹚+2分之1cd-2e0次方的值 2020-11-18 …