早教吧作业答案频道 -->数学-->
已知方程ln|x|-ax2+32=0有4个不同的实数根,则实数a的取值范围是()A.(0,e22)B.(0,e22]C.(0,e23)D.(0,e23]
题目详情
已知方程ln|x|-ax2+
=0有4个不同的实数根,则实数a的取值范围是( )3 2
A. (0,
)e2 2
B. (0,
]e2 2
C. (0,
)e2 3
D. (0,
]e2 3
▼优质解答
答案和解析
由ln|x|-ax2+
=0得ax2=ln|x|+
,
∵x≠0,
∴方程等价为a=
,
设f(x)=
,
则函数f(x)是偶函数,
当x>0时,f(x)=
,
则f′(x)=
=
=
,
由f′(x)>0得-2x(1+lnx)>0,得1+lnx<0,即lnx<-1,得0<x<
,此时函数单调递增,
由f′(x)<0得-2x(1+lnx)<0,得1+lnx>0,即lnx>-1,得x>
,此时函数单调递减,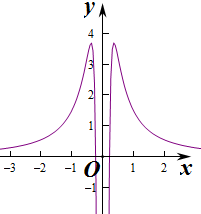
即当x>0时,x=
时,函数f(x)取得极大值f(
)=
=(-1+
)e2=
e2,
作出函数f(x)的图象如图:
要使a=
,
有4个不同的交点,
则满足0<a<
e2,
故选:A
| 3 |
| 2 |
| 3 |
| 2 |
∵x≠0,
∴方程等价为a=
ln|x|+
| ||
| x2 |
设f(x)=
ln|x|+
| ||
| x2 |
则函数f(x)是偶函数,
当x>0时,f(x)=
lnx+
| ||
| x2 |
则f′(x)=
| ||||
| x4 |
| x-2xlnx-3x |
| x4 |
| -2x(1+lnx) |
| x4 |
由f′(x)>0得-2x(1+lnx)>0,得1+lnx<0,即lnx<-1,得0<x<
| 1 |
| e |
由f′(x)<0得-2x(1+lnx)<0,得1+lnx>0,即lnx>-1,得x>
| 1 |
| e |

即当x>0时,x=
| 1 |
| e |
| 1 |
| e |
ln
| ||||
(
|
=(-1+
| 3 |
| 2 |
| 1 |
| 2 |
作出函数f(x)的图象如图:
要使a=
ln|x|+
| ||
| x2 |
有4个不同的交点,
则满足0<a<
| 1 |
| 2 |
故选:A
看了已知方程ln|x|-ax2+3...的网友还看了以下:
下列说法中正确的是()A.因为位移大小和路程不一定相等,所以位移才不等于路程B.位移的大小等于路程 2020-05-14 …
下列说法中正确的是()A.因为位移大小和路程不一定相等,所以位移才不等于路程B.位移的大小等于路程 2020-05-14 …
下列有关说法不正确的是()A.可以利用电解的方法,从海水中获取淡水资源B.以海水为原料,制备金属镁 2020-05-14 …
氯气 水和石灰石制取漂白粉的化学方程式方程式是不是Cl2+H2O+CaCO3这是书上的习题,书上说 2020-05-15 …
从含有两件正品a,b和一件次品c的3件产品中每次任取一件,连续取两次,求取出的两件产品中恰有一件事 2020-06-27 …
玫瑰精油可以使用有机溶剂萃取,但方法有不足之处是下面哪项()A.过程复杂且出油率不高B.提取的玫瑰 2020-07-03 …
初中数学:一元一次不等式(在线等)已知关于X的方程X-A/2=2X+1/3-11.当A取何值时,方 2020-07-14 …
二元一次方程取值范围是怎样求我想知道二元一次方程的非负整数的取值范围怎样求2x+y=9x,y为非负 2020-07-29 …
数学题高分求助,老妹考试要用,第一个大对给100分某同学参加3门课程考试,假设该同学第一门课程取得优 2020-11-20 …
某同学参加某高校自主招生3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为45,第二、第三门课 2020-12-21 …