早教吧作业答案频道 -->数学-->
已知圆C:x2+y2-2x-2y+1=0,直线l:3x+4y-17=0.若在直线l上任取一点M作圆C的切线MA,MB,切点分别为A,B,则AB的长度取最小值时直线AB的方程为.
题目详情
已知圆C:x2+y2-2x-2y+1=0,直线l:3x+4y-17=0.若在直线l上任取一点M作圆C的切线MA,MB,切点分别为A,B,则AB的长度取最小值时直线AB的方程为___.
▼优质解答
答案和解析
当AB的长度最小时,圆心角∠ACB 最小,设为2θ,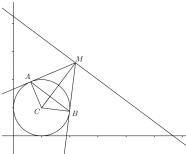
则由cosθ=
=
,
知当θ 最小时,cosθ 最大,即CM 最小,那么CM⊥l,
∴kAB=kl=-
,
设直线AB的方程为3x+4y=m.
又由CM=2,知点C 到直线AB的距离为
,
即
=
,解得m=
或m=
;
经检验m=
,则直线AB的方程为6x+8y-19=0.
故答案为:6x+8y-19=0.

则由cosθ=
| AC |
| CM |
| 1 |
| CM |
知当θ 最小时,cosθ 最大,即CM 最小,那么CM⊥l,
∴kAB=kl=-
| 4 |
| 3 |
设直线AB的方程为3x+4y=m.
又由CM=2,知点C 到直线AB的距离为
| 1 |
| 2 |
即
| 1 |
| 2 |
| |3+4-m| |
| 5 |
| 19 |
| 2 |
| 9 |
| 2 |
经检验m=
| 19 |
| 2 |
故答案为:6x+8y-19=0.
看了已知圆C:x2+y2-2x-2...的网友还看了以下:
过抛物线x2=4y焦点F的直线l与抛物线交于AB,若|BF|,|FA|,|BA|成等差数列,求直线 2020-04-27 …
a为晨昏线,b为纬线,m点为a线的纬度最北点,mn在同一经线上,且纬度差为90°,此时北京为国庆节 2020-05-14 …
已知抛物线x2=-4y过点M(0,-4)的直线与抛物线相交于AB两点(1)求证以AB为直径的圆过原 2020-05-23 …
已知抛物线x2=4y,点P是抛物线上的动点,点A的坐标为(12,6),求点P到点A的距离与到x轴的 2020-06-06 …
抛物线x方=4y,焦点F,过点p〔1,5〕的直线与抛物线交于AB两点,p恰好为ab中点求af+bf 2020-06-10 …
如图,过抛物线x2=4y焦点的直线依次交抛物线与圆x2+(y-1)2=1于点A、B、C、D,则|A 2020-07-20 …
已知抛物线x^2=4y过点m(0,2)作直线l与抛物线交于a,b两点aob面积最小值 2020-07-26 …
抛物线C的方程为x²=4y,过点P(0,-1)作斜率为k(k>0)的直线交抛物线于不同两点A,(1 2020-08-01 …
数学题若干……%>>>梯形ABCD中,AD平行于BC,AB=CD=AD=1,角B=60度.直线MN是 2020-11-18 …
已知A,B两点在抛物线C:x^2=4Y上,点M(0,4)满足向量MA=K向量BM.1)求证:向量已知 2021-02-05 …