早教吧作业答案频道 -->数学-->
如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点C,点D的对应点为点G.则△CEF的面积
题目详情
如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点C,点D的对应点为点G.则△CEF的面积___.
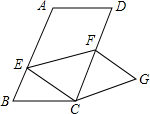

▼优质解答
答案和解析
∵四边形ABCD是平行四边形,
∴AD=BC,∠D=∠B,∠A=∠BCD,
由折叠可知,AD=CG,∠D=∠G,∠A=∠ECG,
∴BC=GC,∠B=∠G,∠BCD=∠ECG,
∴∠BCE=∠GCF,
在△BCE和△GCF中,
,
∴△BCE≌△GCF(ASA),
∴CE=CF,
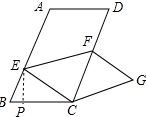
过E点作EP⊥BC于P,如图所示:
∵∠B=60°,∠EPB=90°,
∴∠BEP=30°,
∴BE=2BP,
设BP=m,则BE=2m,
∴EP=BE•sin60°=2m×
=
m,
由折叠可知,AE=CE,
∵AB=6,
∴AE=CE=6-2m,
∵BC=4,
∴PC=4-m,
在RT△ECP中,由勾股定理得(4-m)2+(
m)2=(6-2m)2,
解得:m=
,
∴CE=6-2m=6-2×
=
,
∵△BCE≌△GCF,
∴CF=CE=
,
∴S△CEF=
×
×2
=
;
故答案为:
∴AD=BC,∠D=∠B,∠A=∠BCD,
由折叠可知,AD=CG,∠D=∠G,∠A=∠ECG,
∴BC=GC,∠B=∠G,∠BCD=∠ECG,
∴∠BCE=∠GCF,
在△BCE和△GCF中,
|

∴△BCE≌△GCF(ASA),
∴CE=CF,
过E点作EP⊥BC于P,如图所示:
∵∠B=60°,∠EPB=90°,
∴∠BEP=30°,
∴BE=2BP,
设BP=m,则BE=2m,
∴EP=BE•sin60°=2m×
| ||
| 2 |
| 3 |
由折叠可知,AE=CE,
∵AB=6,
∴AE=CE=6-2m,
∵BC=4,
∴PC=4-m,
在RT△ECP中,由勾股定理得(4-m)2+(
| 3 |
解得:m=
| 5 |
| 4 |
∴CE=6-2m=6-2×
| 5 |
| 4 |
| 7 |
| 2 |
∵△BCE≌△GCF,
∴CF=CE=
| 7 |
| 2 |
∴S△CEF=
| 1 |
| 2 |
| 7 |
| 2 |
| 3 |
7
| ||
| 2 |
故答案为:
7
| ||
| 2 |
作业帮用户
2017-01-19
举报

看了 如图,在平行四边形ABCD中...的网友还看了以下:
如图,在梯形纸片ABCD中,BC//AD,∠A+∠D=90°,tanA=2.过B点作BH⊥AD于H. 2020-03-30 …
进行下列数的数制转换(213)D=()B=()H=()O(69.625)D=()B=()H=()O 2020-05-21 …
质量为m的苹果,从距地面高度为H的树上由静止开始落下,树下有深度为h的坑.若以地面为参考平面,则当 2020-06-04 …
(2006•南宁)如图是一个等边三角形木框,甲虫P在边框AC上爬行(A,C端点除外),设甲虫P到另 2020-07-12 …
下列句子没有古今异义的一项是()A.君子博学而日参省乎己B.蚓无爪牙之利,筋骨之强C.锲而舍之,朽 2020-07-15 …
进制换算(213)D=()B=()H=()O(69.625)D=()D=()B=()O(127)D 2020-07-19 …
如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分,这点叫做这条折线的 2020-07-25 …
推断题:现有如下反应(反应条件均不给),推断物质⑴A→B+C+D⑵C+E→C+F+D⑶D+G→H⑷ 2020-07-30 …
如下图所示,已知矩形ABCD中,AB=3,BC=4,将矩形折叠使C点与A点重合。(1)作出折痕EF, 2020-11-06 …
有一种无毒蛇的体表花纹颜色由D、d和H、h两对基因(独立遗传)控制,与性别无关.其花纹颜色与基因的对 2020-12-08 …