早教吧作业答案频道 -->数学-->
设各项均为正数的数列{an}的前n项和为Sn,满足,且a2,a5,a14构成等比数列.(1)证明:;(2)求数列{an}的通项公式;(3)证明:对一切正整数n,有.
题目详情
设各项均为正数的数列{a n }的前n项和为S n ,满足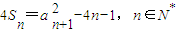 ,且a 2 ,a 5 ,a 14 构成等比数列.
,且a 2 ,a 5 ,a 14 构成等比数列.
(1)证明: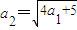 ;
;
(2)求数列{a n }的通项公式;
(3)证明:对一切正整数n,有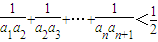 .
.
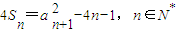 ,且a 2 ,a 5 ,a 14 构成等比数列.
,且a 2 ,a 5 ,a 14 构成等比数列.(1)证明:
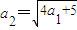 ;
;(2)求数列{a n }的通项公式;
(3)证明:对一切正整数n,有
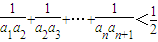 .
.▼优质解答
答案和解析
分析:
(1)对于,令n=1即可证明;(2)利用,且,(n≥2),两式相减即可求出通项公式.(3)由(2)可得=.利用“裂项求和”即可证明.
(1)当n=1时,,∵(2)当n≥2时,满足,且,∴,∴,∵an>0,∴an+1=an+2,∴当n≥2时,{an}是公差d=2的等差数列.∵a2,a5,a14构成等比数列,∴,,解得a2=3,由(1)可知,,∴a1=1∵a2-a1=3-1=2,∴{an}是首项a1=1,公差d=2的等差数列.∴数列{an}的通项公式an=2n-1.(3)由(2)可得式=.∴
点评:
熟练掌握等差数列与等比数列的通项公式、“裂项求和”、通项与前n项和的关系an=Sn-Sn-1(n≥2)是解题的关键.
分析:
(1)对于,令n=1即可证明;(2)利用,且,(n≥2),两式相减即可求出通项公式.(3)由(2)可得=.利用“裂项求和”即可证明.
(1)当n=1时,,∵(2)当n≥2时,满足,且,∴,∴,∵an>0,∴an+1=an+2,∴当n≥2时,{an}是公差d=2的等差数列.∵a2,a5,a14构成等比数列,∴,,解得a2=3,由(1)可知,,∴a1=1∵a2-a1=3-1=2,∴{an}是首项a1=1,公差d=2的等差数列.∴数列{an}的通项公式an=2n-1.(3)由(2)可得式=.∴
点评:
熟练掌握等差数列与等比数列的通项公式、“裂项求和”、通项与前n项和的关系an=Sn-Sn-1(n≥2)是解题的关键.
看了 设各项均为正数的数列{an}...的网友还看了以下:
运用反证法,证明圆的相切线垂直圆用反证法。切线过切点,且切点到圆心的距离为圆的半径。如果切点与圆心 2020-06-09 …
古汉字注音“××切怎么读?”我发现在《说文解字》上几乎所有的汉字注音都是“××切”,这个怎么拼?听 2020-06-15 …
一个长方体的长宽高都是整厘米数把它切割成两个完全一模一样的小长方体一个长方体的长宽高都是整米数把它 2020-06-15 …
国际上钻石的重量计量单位为克拉.已知某种钻石的价值v(美元)与其重量w(克拉)的平方成正比,且一颗 2020-06-30 …
已知点是圆内一点,直线l是以M为中点的弦所在的直线,直线m的方程为,那么A.且m与圆C相切B.且/ 2020-07-26 …
过点Q(-2,√21)作圆C:x^2+y^2=r^2(r>0)的切线,切点为D,且QD=4.(1) 2020-07-31 …
过点Q(-2,√21)作圆C:x^2+y^2=r^2(r>0)的切线,切点为D,且QD=4.求:设 2020-07-31 …
在平面直角坐标系xoy中y=3/4x+3,与x轴交于A,与y轴交于B,⊙P与x轴相切且与y=3/4x 2020-11-03 …
设曲线上任一点处的切线斜率与切点的横坐标成反比,且曲线过点(1,2)求该曲线的方程. 2020-11-29 …
宇宙大爆炸和黑洞,白洞还有虫洞的关系如果黑洞吸进一切物体,且在假设白洞存在的前提下,由白洞喷射出被黑 2020-12-24 …