早教吧作业答案频道 -->数学-->
在等腰直角三角形中,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.(1)说明:BE2+CF2=EF2;(2)若BE=12,CF=5,试求△DEF的面积.
题目详情
在等腰直角三角形中,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
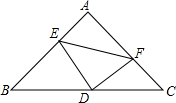
(1)说明:BE2+CF2=EF2;
(2)若BE=12,CF=5,试求△DEF的面积.

(1)说明:BE2+CF2=EF2;
(2)若BE=12,CF=5,试求△DEF的面积.
▼优质解答
答案和解析
(1)证明:连接AD,如图所示: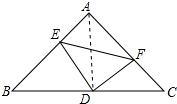
∵AB=AC,D为BC的中点,∠BAC=90°,
∴AD⊥BC,AD=CD=BD,∠C=∠B=45°,∠DAE=45°,
∵DE⊥DF,
∴∠CDF+∠ADF=∠EDA+∠ADF,
即∠CDF=∠ADE,
在△DCF和△ADE中,
,
∴△DCF≌△ADE(ASA),
∴CF=AE,DF=DE,
∴BE=AF,
∵AF2+AE2=EF2,
∴BE2+CF2=EF2;
(2) 由(1)知:AE=CF=5,同理AF=BE=12,
∵∠EAF=90°,
∴EF2=AE2+AF2=52+122=169,
∴EF=13,
又∵由(1)知:△AED≌△CFD,
∴DE=DF,
∴△DEF为等腰直角三角形,
∴DE=DF=EF•
=
,
∴△DEF的面积=
DE2=
.

∵AB=AC,D为BC的中点,∠BAC=90°,
∴AD⊥BC,AD=CD=BD,∠C=∠B=45°,∠DAE=45°,
∵DE⊥DF,
∴∠CDF+∠ADF=∠EDA+∠ADF,
即∠CDF=∠ADE,
在△DCF和△ADE中,
|
∴△DCF≌△ADE(ASA),
∴CF=AE,DF=DE,
∴BE=AF,
∵AF2+AE2=EF2,
∴BE2+CF2=EF2;
(2) 由(1)知:AE=CF=5,同理AF=BE=12,
∵∠EAF=90°,
∴EF2=AE2+AF2=52+122=169,
∴EF=13,
又∵由(1)知:△AED≌△CFD,
∴DE=DF,
∴△DEF为等腰直角三角形,
∴DE=DF=EF•
| ||
| 2 |
13
| ||
| 2 |
∴△DEF的面积=
| 1 |
| 2 |
| 169 |
| 4 |
看了 在等腰直角三角形中,AB=A...的网友还看了以下:
原子核x衰变为原子核Y再衰变为原子核Z的过程如下:abXβcdYαefZ下述各关系式中正确的是() 2020-04-05 …
如图,点D、B分别在∠A的两边上,C是∠A内一点,且AB=AD,BC=DC,CE⊥AD,CF⊥AB 2020-05-17 …
如图,AB是⊙O的直径,点C为AB上面半圆上一点,点D为AB的下面半圆的中点,连接CD与AB交于点 2020-05-17 …
如图,点D、B分别在∠A的两边上,C是∠A内一点,且AB=AD,BC=DC,CE⊥AD,CF⊥AB 2020-05-21 …
如图,AB∥DE,试问∠B、∠E、∠BCE有什么关系.解:∠B+∠E=∠BCE过点C作CF∥AB, 2020-06-12 …
如图,直线MN经过正方形ABCD的一个顶点A,过点B作BE⊥MN于点E,过点C作CF⊥MN于点F, 2020-06-22 …
(1)阅读填空:如图1,AB∥DE,试问∠B、∠E、∠BCE有什么关系.解:∠B+∠E=∠BCE过 2020-07-22 …
在正方形ABCD中,E为CD上一点,连接AE,过点C作CF⊥AF的延长线于点F,连接DF,过点D作 2020-08-01 …
已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF 2020-08-03 …
在△ABC中,∠ACB=2∠B,∠BAC的平分线AD交BC于点D.(1)如图1,过点C作CF⊥AD于 2020-11-01 …